【洛谷P5667】拉格朗日插值2 | Mrsrz's blog

下降幂平移

题目大意：

给定一个不超过 $n$ 次的多项式在 $n+1$ 个点的点值 $f(0),f(1),f(2),\dots,f(n)$，给出 $m$。

求 $f(m),f(m+1),f(m+2),\dots,f(m+n)$ 的值。

题解：

本题可以将点值转化为下降幂系数，然后做一次下降幂多项式平移，再转化为点值。

关于如何将点值与下降幂系数互相转化，详见下降幂多项式乘法的模板。

这里主要讨论下降幂多项式的平移。

这里的平移指的是，已知多项式 $f(x)$ 的各项系数并给定常数 $c$，求 $f(x+c)$ 的各项系数。

这里需要用到下降幂的二项式定理。

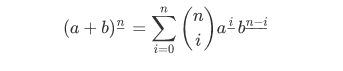
《具体数学》习题5.37

考虑我们当前得到 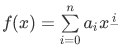，对 $f(x+c)$ 进行分析。

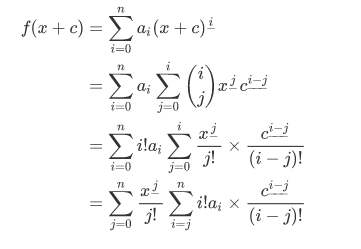
观察这个式子 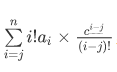，这是可以用一次多项式乘法得到的。

令

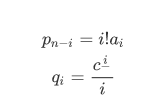
那么 $f(x+c)$ 的第 $k$ 项下降幂系数就是 $p$ 与 $q$ 的卷积的第 $n-k$ 项，还要乘上 $k!$ 的逆。

得到 $f(x+c)$ 的下降幂系数后，再转化成点值即可。

总共需要三次多项式乘法。

时间复杂度 $O(n\log n)$。

Code：

#include<iostream>
#include<algorithm>
using namespace std;
const int N=524288,md=998244353,g3=(md+1)/3;
typedef long long LL;
int a[N],n,rev[N],lim,m,fac[N],iv[N],F[N];
inline void upd(int&a){a+=a>>31&md;}
inline int pow(int a,int b){
    int ret=1;
    for(;b;b>>=1,a=(LL)a*a%md)if(b&1)ret=(LL)ret*a%md;
    return ret;
}
void init(int n){
    int l=-1;
    for(lim=1;lim<n;lim<<=1)++l;
    for(int i=1;i<lim;++i)
        rev[i]=(rev[i>>1]>>1)|((i&1)<<l);
}
void FFT(int*a,int f){
    for(int i=1;i<lim;++i)
        if(i<rev[i])swap(a[i],a[rev[i]]);
    for(int i=1;i<lim;i<<=1){
        const int gi=pow(f?3:g3,(md-1)/(i<<1));
        for(int j=0;j<lim;j+=i<<1)
            for(int k=0,g=1;k<i;++k,g=(LL)g*gi%md){
                const int x=a[j+k],y=a[j+k+i]*(LL)g%md;
                upd(a[j+k]+=y-md),upd(a[j+k+i]=x-y);
            }
    }
    if(!f){
        const int vv=pow(lim,md-2);
        for(int i=0;i<lim;++i)a[i]=(LL)a[i]*vv%md;
    }
}
int main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>m;++n;
    for(int i=0;i<n;++i)cin>>a[i];
    for(int i=*fac=1;i<=n;++i)fac[i]=(LL)fac[i-1]*i%md;
    iv[n]=pow(fac[n],md-2);
    for(int i=n-1;~i;--i)iv[i]=(i+1LL)*iv[i+1]%md;
    for(int i=0;i<n;++i)
        a[i]=(LL)a[i]*iv[i]%md,F[i]=(i&1)?md-iv[i]:iv[i];
    init(n<<1);
    FFT(a,1),FFT(F,1);
    for(int i=0;i<lim;++i)a[i]=(LL)a[i]*F[i]%md;
    FFT(a,0);
    for(int i=n;i<lim;++i)a[i]=F[i]=0;
    F[0]=1;
    for(int i=1;i<n;++i){
        F[i]=(LL)F[i-1]*(m-i+1)%md;
        a[i]=(LL)a[i]*fac[i]%md;
    }
    reverse(a,a+n);
    for(int i=1;i<n;++i)
        F[i]=(LL)F[i]*iv[i]%md;
    FFT(a,1),FFT(F,1);
    for(int i=0;i<lim;++i)a[i]=(LL)a[i]*F[i]%md;
    FFT(a,0);
    for(int i=n;i<lim;++i)a[i]=F[i]=0;
    reverse(a,a+n);
    for(int i=0;i<n;++i)F[i]=iv[i],a[i]=(LL)a[i]*iv[i]%md;
    FFT(a,1),FFT(F,1);
    for(int i=0;i<lim;++i)a[i]=(LL)a[i]*F[i]%md;
    FFT(a,0);
    for(int i=0;i<n;++i)
        cout<<(LL)a[i]*fac[i]%md<<' ';
    cout<<'\n';
    return 0;
}