【洛谷P5600】【XR-4】尺规作图
提交答案题
题目大意:
给定平面上一些点,和一些已知线段、直线、圆,要得到某个指定的点。
能做的操作有两种:
- 指定两个已经得到的点,过这两点作直线。
- 指定两个已经得到的点,以某个点为圆心,另一个点为圆上一点,画圆。
一个点已经得到,当且仅当其在输入中给出,或是两条线的交点。
有 $10$ 个任务。
题解:
使用了传统题的提交方式,但它还是一道提交答案题。
挺有趣的一题,是真的要尺规作图。
这个网站可以辅助解题。
先做一些约定,令 直线AB 表示过 A 点和 B 点的直线,圆AB 表示以 A 为圆心,AB 长为半径的圆。
下面对每个点分别进行讨论。所有有图解的点都会结合图解进行解释。
任务一
给定一条线段,求其中点。
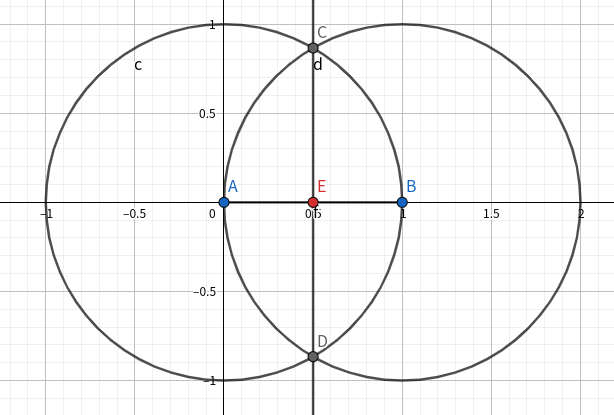
非常简单,作 圆AB 和 圆BA,过两圆交点作 直线CD,与线段交点 E 即为所求。如图所示。
任务二
给定 $\rm A(0,0), B(1,0)$ ,直线AB($x$ 轴) 以及直线外一点 C,过 点C 作 直线AB 的垂线,求垂足。
也比较简单,作 圆AC,交 直线AB 于D,作 圆DC,与 圆AC 交于 E。作 直线CE,与 直线AB 的交点即为所求。如图所示。

任务三
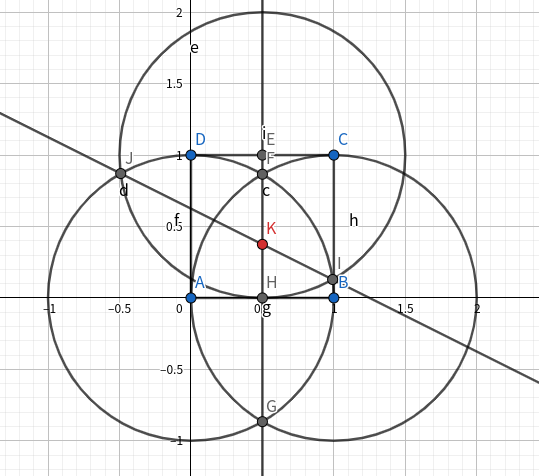
给定 正方形ABCD 的四个点和四条边,求其内部一个点,到 A,B ,线段CD 的距离均相等。
到线段两点的距离相等,不难想到作中垂线。这里就是求两条中垂线的交点。
作 线段AB 的中垂线的同时即求得 线段BC 的中点 E 以及 线段AB 的中点 F。这里花费 $3$ 步。
现在要作 线段AE(无需连接) 的中垂线,只剩两步了,怎么办?
我们考虑共用之前的一个圆。由于是正方形,所以有 $\rm AD=EF$。
由于作中垂线只需要分别以两个端点为圆心,任意长度为半径作圆,保证有两个交点就可以。所以我们一开始做 线段AB 的中垂线的时候,以 $\rm AB$ 为半径作 圆AB 和圆 BA。这里只需作 圆EF,与 圆AB 交于 I 和 J。再作 直线IJ 即为 线段AE 的中垂线。那么 直线IJ 与直线 EF 的交点即为所求。
总共 $5$ 步。
如图所示。
任务四
给定 $\rm A(0,0)$ 和 $\rm B(1,0)$ 以及 直线AB,要求作出 $(1024,0)$。
我们通过作 圆BA,与 直线AB 交于 $(2,0)$,再以这个交点为圆心,横坐标为半径做圆。这样每次交出来的点是原来的 $2$ 倍。因此作 $10$ 次即可得到 $(1024,0)$。
任务五
给定 $\rm A(0,0)$ 和 $\rm B(1,0)$ 以及 直线AB,要求作出 $(1000,0)$。
沿着任务四的思路,还是考虑用倍增的方法。
这里可以不每次以横坐标为半径作圆。由于我们有 $(1,0)$,所以点 $(x,0)$ 可以通过作半径为 $x-1$ 的圆,来得到 $(2x-1,0)$。
所以按照以下方法即可:
共计 $10$ 步。
任务六
给定 $\rm A(0,0),B(0,1)$ 以及单位圆,求圆上某一点。
这个点的思路是,求出所求点与原点的直线,与单位圆的交点即为所求。
这条直线的斜率约为 $k=0.465440612$。我们需要找到一个整点,使得其与原点的直线的斜率大致为这个数。
我找到这个点 $(6525,3037)$,其斜率约为 $0.465440613$,在 Deepin 的计算器所示精度下只有最后一位有误差。
然后我们通过任务五的倍增方法(可以稍微进行一些改进)得到 $(6525,0)$ 以及 $(0,3037)$ ,然后得到这两个点连接而成的线段的中点(作中垂线即可),与原点作直线即可。
这里花了 $32$ 步。
任务七
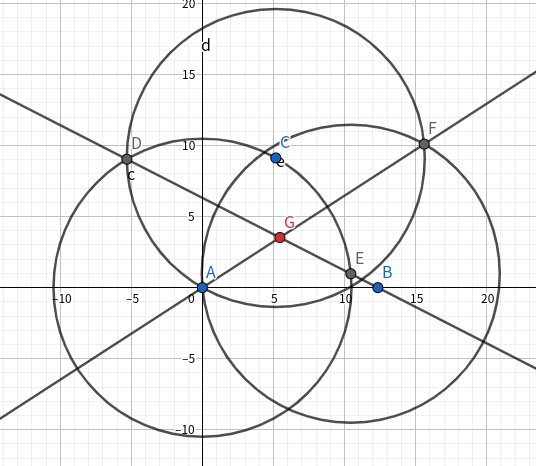
给定锐角三角形的三个点,求其费马点。
按照传统费马点的做法,是要向外做等边三角形的。我按照这个思路试了试,步数显然过多。
然后去掉了一些操作,瞎试了一下就做出来了。。
放图解吧。
任务八
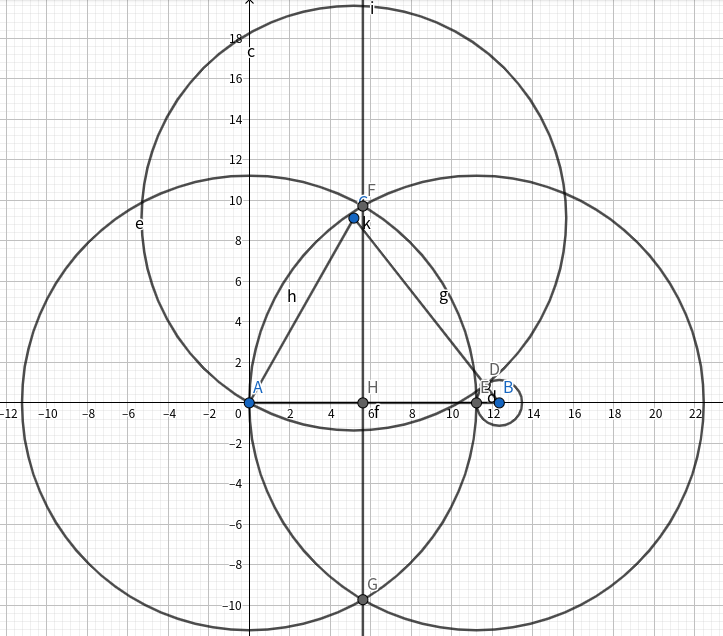
给定三角形,求其内切圆与某一边的切点。
如图所示,设三边长分别 $f,g,h$。
由切线长定理可知,切点到某个端点的距离为 $\frac{f+g-h}{2}$。
首先作 圆CA,交 线段BC 于 D。那么得到 $\rm BD=h-g$。
然后作 圆BD,交 线段AB 于 E。那么得到 $BE=h-g$,则 $AE=f+g-h$。
再花三步作 线段AE 的中垂线即可。
任务九
给定两点,求一个奇怪的点。
这个……我也不知道如何解释。胡乱试一下就试出来了。
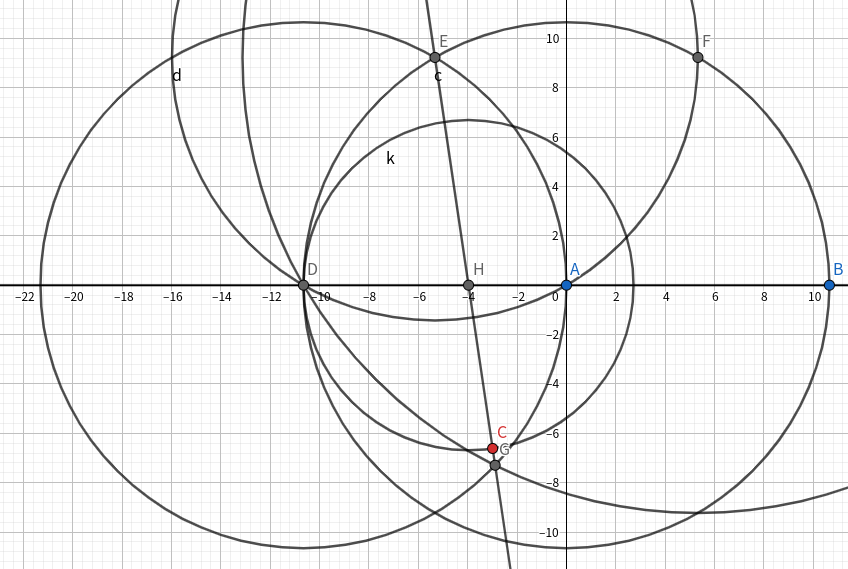
任务十
给定任务九中的两点,求另一个奇怪的点。
考虑在任务九的基础上继续。
如图所示(与任务九的有所不同),发现所求 点C 与 J 和 F 共线。
然后再瞎尝试一波……
如图,作 直线KL,交 圆AB 于 点M。
再作 圆MN,与 直线FJ 的另一交点即为所求…………
奥妙重重
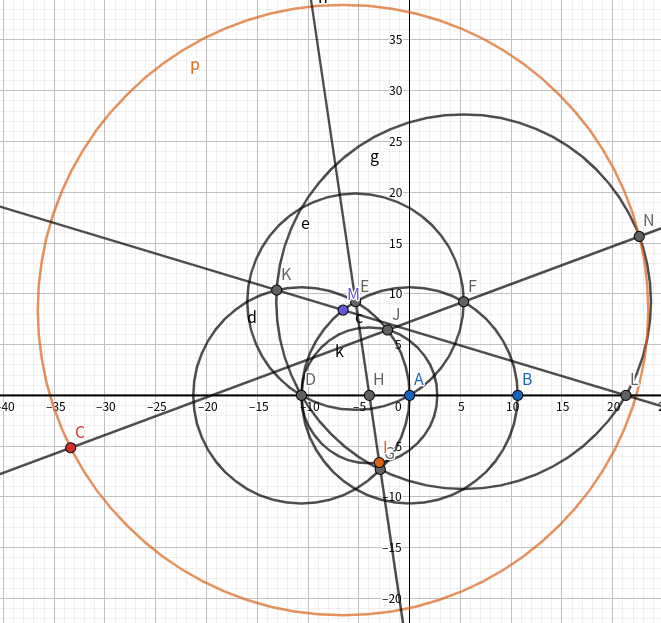
下面是提交代码,所有任务的答案都整合在里面。
Code:
#include<iostream>
using namespace std;
int main(){
int id;
cin>>id;
if(id==1)
cout<<R"(3
1 0 0 1 0
1 1 0 0 0
2 0.5 0.866025404 0.5 -0.866025404
)";
if(id==2)
cout<<R"(3
1 0 0 5.23124577 4.31624417
1 6.7820274285203 0 5.23124577 4.31624417
2 5.23124577 4.31624417 5.23124577 -4.31624417
)";
if(id==3)
cout<<R"(5
1 0 0 0 1
1 1 0 1 1
2 0.5 0.86602540378 0.5 -0.86602540378
1 0.5 1 0.5 0
2 -0.49161985 0.87080992 0.9916198487 0.1291900756
)";
if(id==4)
cout<<R"(10
1 1 0 0 0
1 2 0 0 0
1 4 0 0 0
1 8 0 0 0
1 16 0 0 0
1 32 0 0 0
1 64 0 0 0
1 128 0 0 0
1 256 0 0 0
1 512 0 0 0
)";
if(id==5)
cout<<R"(10
1 1 0 0 0
1 2 0 0 0
1 4 0 0 0
1 8 0 0 0
1 16 0 0 0
1 32 0 1 0
1 63 0 1 0
1 125 0 0 0
1 250 0 0 0
1 500 0 0 0
)";
if(id==6)
cout<<R"(32
2 0 0 0 1
1 0 1 0 -1
1 0 -1 0 1
2 1.73205080 0 -1.73205080 0
1 0 3 0 0
1 0 6 0 0
1 0 12 0 -1
1 0 25 0 0
1 0 50 0 -1
1 0 101 0 -1
1 0 203 0 -1
1 0 407 0 -1
1 0 815 0 -1
1 0 1631 0 0
1 0 3262 0 -1
1 0 1 0 0
1 0 2 0 -1
1 0 5 0 -1
1 0 11 0 -1
1 0 23 0 -1
1 0 47 0 0
1 0 94 0 -1
1 0 189 0 -1
1 0 379 0 -1
1 0 759 0 0
1 0 1518 0 -1
1 0 0 0 6525
1 6525 0 0 3037
1 0 3037 6525 0
2 632.38084870666 -4132.31575969 5892.6191512933 7169.31575969
2 6525 0 0 3037
2 0 0 3262.500000 1518.500000
)";
if(id==7)
cout<<R"(5
1 0 0 5.16457145 9.12243565
1 5.16457145 9.12243565 0 0
2 12.34441574 0 -5.317975292288 9.0338679003
1 10.4374465400 0.97536669 0 0
2 0 0 15.6020179900 10.09780234
)";
if(id==8)
cout<<R"(5
1 5.16457145 9.12243565 0 0
1 12.34441574 0.00000000 11.6479643 0.88488458
1 0 0 11.218331671 0
1 11.218331671 0 0 0
2 5.609165835 9.7153602149 5.609165835 -9.7153602149
)";
if(id==9)
cout<<R"(6
1 0 0 10.64978745 0
1 -10.64978745 0 0 0
1 -5.324893725 9.22298647 0 0
1 5.324893725 9.22298647 -10.64978745 0
2 -5.324893725 9.22298647 -2.88914298926 -7.29317285
1 -3.96471696441 0 -10.64978745 0
)";
if(id==10)
cout<<R"(9
1 0 0 10.64978745 0
1 -10.64978745 0 0 0
1 -5.324893725 9.22298647 0 0
1 5.324893725 9.22298647 -10.64978745 0
2 -5.324893725 9.22298647 -2.88914298926 -7.29317285
1 -3.96471696441 0 -10.64978745 0
2 5.324893725 9.222986477 -2.16685724 6.43877844
2 -13.08553819 10.367501679 21.2995749 0
1 -6.5503572407083 8.39707049 22.61544124 15.6487849
)";
return 0;
}
