【Ynoi2013】对数据结构的爱/【Codeforces 1172F】Nauuo and Bug
线段树维护分段函数
题目大意:
给你如下伪代码:

给定 $p$ 和数列 $a$,有 $m$ 组询问,每次给定 $l,r$,问 sum(a,l,r,p) 的值是多少。
题解:
考虑当前的数为 $v$,经过连续一段数后,变成了 $f(v)$。这个 $f(v)$ 是一个分段函数,每段是一个一次函数,且一次项系数为 $1$。
对 $n$ 个数的分段函数,分成的段数为 $n+1$。考虑当 $n=1$ 的如下情况:
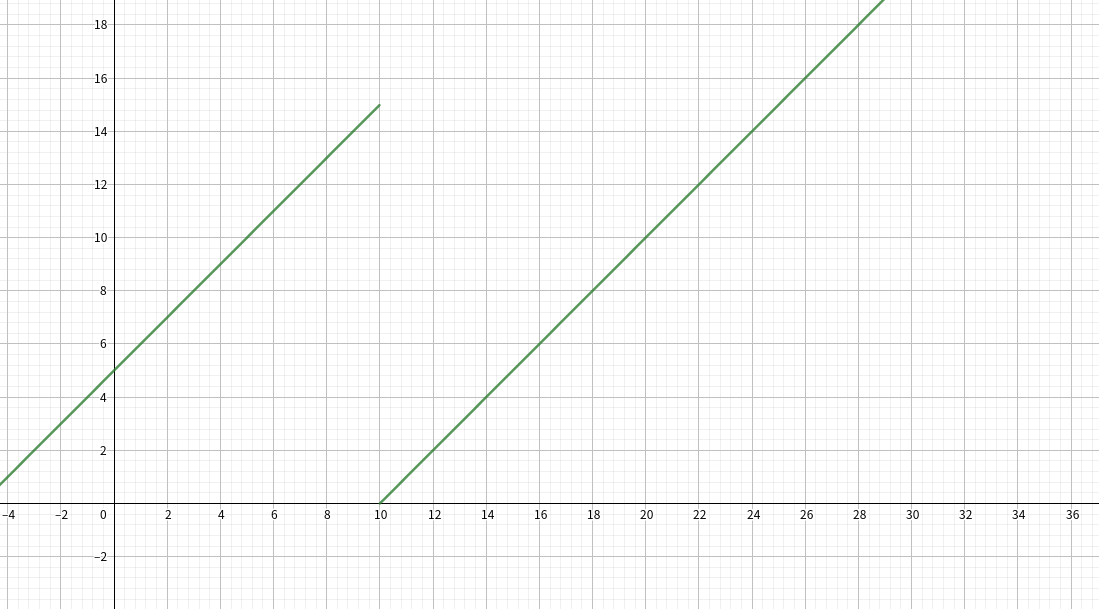
考虑要新加上一个数并执行modadd操作。那么,分段函数所有在 $p$ 及以上的部分,都会整体下移 $p$。
想象一下,前 $n$ 段,每段超过 $p$ 的部分,下移后一定会和下一段恰好连接起来,形成新的一段。然后最后那段值域到 $+\infty$ 的部分,下移后会形成新的一段,所以会新增一段。
考虑用线段树维护每个区间的数的分段函数。查询的时候,在线段树结点的分段函数上二分所在段,得到当前的数经过这个区间后会变成的数字即可。单次查询的复杂度为 $O(\log^2 n)$。
考虑构造这棵线段树,用二分的方法把左边和右边复合的时间复杂度是 $O(n\log^2 n)$ 的,无法通过。
我们发现,分段函数每段的长度都至少为 $p$。仔细思考分段函数上下移动的过程,如果遇到的一直是加操作,那么一段被截到下一部分,必定有一段等长的从上一段补过来,所以中间的那些段都有相同的高度 $h$。如果遇到减操作,那么最后一段的高度会高于 $h$,而中间段,最高高度仍不变。由于斜率为 $1$,每段纵坐标差至少为 $p$,故横坐标覆盖的范围也是 $p$。
那么我们复合两段函数的时候,按横坐标从小到大的顺序枚举左边的 $f$,并用一个指针指向当前 $f$ 函数值对应的右边 $g$ 的段。然后,$f$ 的下一段和当前段的函数值相差为 $p$,所以 $g$ 的指针最多只需往前移动 $1$。所以总的复杂度是线性的。
那么维护区间的分段函数的复杂度降为 $O(n\log n)$。
总时间复杂度 $O(n\log n+m\log^2 n)$。
由于线段树每层需要记录 $O(n)$ 个信息,所以空间复杂度 $O(n\log n)$。
Code:
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
const LL inf=5e16;
const int N=1.1e6;
struct func{
LL r,b;
inline LL operator()(LL x){return x+b;}
inline bool operator<(const func&rhs)const{return r<rhs.r;}
};
func*d[N<<1];
int n,m,md,sz[N<<1];
void merge(func*&h,func*F,func*g,int&szh,const int&szf,const int&szg){
static func sta[N<<1],f[N<<1];int top=0;sta[0].b=inf;
for(int i=0;i<szf;++i)f[i+1]=F[i];f[0].r=-inf;
for(int i=1,it=0;i<=szf;){
const LL L=max(-inf,f[i](f[i-1].r+1)),R=min(inf,f[i](f[i].r));
while(it<szg&&L>g[it].r)++it;
if(R<=g[it].r){
LL b=f[i].b+g[it].b;
if(sta[top].b!=b)
sta[++top]=(func){f[i].r,b};
else
sta[top].r=f[i].r;
++i;
}else{
const LL mid=g[it].r-f[i].b;
LL b=f[i].b+g[it].b;
if(sta[top].b!=b)
sta[++top]=(func){mid,f[i].b+g[it].b};
else
sta[top].r=mid;
f[i-1].r=mid;
}
it-=!!it;
}
h=new func[szh=top];
for(int i=1;i<=top;++i)
h[i-1]=sta[i];
}
void build(int l,int r,int o){
if(l==r){
int x;
cin>>x;
d[o]=new func[sz[o]=2];
d[o][0]=(func){md-x-1,x},d[o][1]=(func){inf,x-md};
}else{
const int mid=l+r>>1;
build(l,mid,o<<1),build(mid+1,r,o<<1|1);
merge(d[o],d[o<<1],d[o<<1|1],sz[o],sz[o<<1],sz[o<<1|1]);
}
}
void trans(int l,int r,int o,const int&L,const int&R,LL&ans){
if(L<=l&&r<=R){
ans=(*(lower_bound(d[o],d[o]+sz[o],(func){ans})))(ans);
}else{
const int mid=l+r>>1;
if(L<=mid)trans(l,mid,o<<1,L,R,ans);
if(mid<R)trans(mid+1,r,o<<1|1,L,R,ans);
}
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m>>md;
build(1,n,1);
while(m--){
LL ans=0;
int l,r;
cin>>l>>r;
trans(1,n,1,l,r,ans);
cout<<ans<<'\n';
}
return 0;
}
