IOI2021集训队作业
IOI2021 集训队作业,持续更新。表格内打 * 的表示还未写题解。
目前完成 132 题,题解会缓(gu)慢(gu)更(gu)新(gu)。
| 试题一 | 完成情况 | 试题二 | 完成情况 | 试题三 | 完成情况 |
|---|---|---|---|---|---|
| UC | ✔(2020.11.12) | DG | ✔(2020.10.29)(*) | RB | ✔(2020.12.1)(*) |
| HC | ✔(2020.11.26)(*) | IB | ✔(2020.11.9) | FJ | ✔(2020.11.20)(*) |
| GK | ✔(2020.11.4) | UH | ✔(2020.11.11)(*) | QH | ✔(2020.11.13)(*) |
| EE | ✔(2020.12.17)(*) | DJ | ✔(2020.12.15)(*) | IH | ✔(2020.12.22)(*) |
| HL | ✔(2020.12.16)(*) | MI | ✔(2020.12.15)(*) | EJ | |
| MB | ✔(2020.11.6)(*) | UI | ✔(2020.11.24)(*) | ED | ✔(2020.10.30)(*) |
| AA | ✔(2020.11.5)(*) | BG | ✔(2020.12.17)(*) | ML | ✔(2020.11.15)(*) |
| CF | ✔(2020.12.7)(*) | TE | QG | ✔(2020.11.21) | |
| PH | ✔(2020.12.24)(*) | UJ | ✔(2020.10.24) | BB | |
| CI | SD | ✔(2020.11.3)(*) | NG | ✔(2020.12.19)(*) | |
| DK | ✔(2020.12.2)(*) | LD | ✔(2020.12.11)(*) | IJ | ✔(2020.11.8) |
| NC | ✔(2021.1.4)(*) | BJ | ✔(2020.11.6)(*) | FK | ✔(2020.11.24)(*) |
| CH | NJ | ✔(2020.11.22)(*) | RH | ✔(2020.12.16) | |
| QF | ✔(2020.10.24) | BE | ✔(2020.11.20)(*) | KI | ✔(2020.11.25)(*) |
| AC | ✔(2020.12.14)(*) | PG | HM | ✔(2020.11.22)(*) | |
| PJ | ✔(2020.11.18)(*) | ID | ✔(2020.12.7)(*) | EG | |
| SI | ✔(2020.11.13)(*) | KC | ✔(2020.12.25)(*) | GI | ✔(2020.11.11)(*) |
| OG | ✔(2020.10.28)(*) | CK | ✔(2020.10.14) | DB | ✔(2020.12.21)(*) |
| QE | ✔(2020.10.14) | GH | ✔(2020.12.28)(*) | NI | ✔(2020.11.10)(*) |
| OL | ✔(2020.10.26)(*) | KA | ✔(2020.12.18)(*) | MG | |
| SG | ✔(2020.11.10)(*) | NL | ✔(2020.12.7)(*) | KH | ✔(2020.10.22) |
| QJ | ✔(2020.12.6) | KG | ✔(2020.12.23)(*) | AB | ✔(2020.12.10)(*) |
| KD | ✔(2020.12.8)(*) | IL | ✔(2020.11.9)(*) | NF | ✔(2020.10.31) |
| CM | ✔(2020.11.27)(*) | NE | ✔(2020.11.15)(*) | HD | ✔(2020.11.18)(*) |
| DH | ✔(2020.12.25)(*) | EC | BM | ✔(2020.11.19)(*) | |
| LC | ✔(2020.12.19)(*) | CD | ✔(2020.11.11)(*) | JI | ✔(2020.11.12)(*) |
| DL | ✔(2020.11.25)(*) | ME | ✔(2020.11.28)(*) | PE | ✔(2020.12.23)(*) |
| LI | ✔(2020.10.13) | AI | ✔(2020.11.16)(*) | RJ | ✔(2020.10.14) |
| SF | ✔(2020.11.13)(*) | II | HG | ✔(2020.12.8)(*) | |
| RE | ✔(2020.10.12) | LL | ✔(2020.10.13) | OA | ✔(2020.12.11)(*) |
| FB | ✔(2020.10.13) | QD | ✔(2020.12.22)(*) | DA | ✔(2020.12.14)(*) |
| TC | ✔(2020.12.28)(*) | AE | ✔(2020.12.18)(*) | CB | ✔(2020.12.14)(*) |
| GF | ✔(2020.12.9)(*) | AG | ✔(2020.11.17)(*) | JC | |
| PA | ✔(2020.12.10)(*) | TH | ✔(2020.12.11) | EH | ✔(2020.11.16)(*) |
| AJ | TK | ✔(2020.10.26) | EI | ✔(2020.10.26)(*) | |
| UL | ✔(2020.12.21)(*) | AF | ✔(2020.12.22)(*) | SK | ✔(2020.12.9)(*) |
| BH | ✔(2020.12.17) | RD | ✔(2020.11.17)(*) | OK | ✔(2020.11.13)(*) |
| FC | JD | ✔(2020.12.21)(*) | OE | ✔(2020.11.20)(*) | |
| TF | ✔(2020.10.27) | FF | DD | ✔(2020.10.23)(*) | |
| CJ | HK | ✔(2020.12.10)(*) | MJ | ✔(2020.11.3)(*) | |
| FG | ✔(2020.10.13) | GL | ✔(2020.11.23)(*) | AL | |
| FI | ✔(2020.11.21)(*) | IC | ✔(2020.11.25)(*) | QC | ✔(2020.11.20) |
| MD | ✔(2020.12.9)(*) | OJ | ✔(2020.10.12) | HI | ✔(2020.12.9)(*) |
| KK | ✔(2020.12.8)(*) | JH | ✔(2020.12.25)(*) | OB | ✔(2020.12.22)(*) |
| BK | ✔(2020.12.24)(*) | GJ | ✔(2020.10.20) | KE | |
| CA | ✔(2020.11.11)(*) | IK | ✔(2020.10.22) | LE | |
| RI | ✔(2020.10.23) | LK | ✔(2020.10.25) | PD | ✔(2020.11.10) |
| JE | ✔(2020.11.29)(*) | LB | ✔(2020.12.7)(*) | HB | ✔(2020.11.18)(*) |
| BL | ✔(2020.10.26) | RG | ✔(2020.10.14) | AH | ✔(2020.12.23)(*) |
| AK | ✔(2020.10.12) | GG | ✔(2020.10.28)(*) | JG | ✔(2020.11.9)(*) |
表格及链接来自兔队。
题目编号规则:由两个字母组成,第一个字母表示该题的来源(详见兔队的博客)。第二个字母表示该题在其所在比赛中的题目编号。
鸽了鸽了,心情好了会补题解
AK
题目大意:
给定一个大小为 $n$ 的环和 $k$ 条线段,要求使用最少的线段覆盖环。
$n,k\le 10^6$。
题解:
记 $A_{i,j}$ 表示位置 $j$ 及其之前开始经过 $2^i$ 轮能到达的最右端点。
上面加粗部分并不影响答案,但是能够使 $A_{\star,j}$ 单调不降。
考虑倍增得到 $A_{i,j}$,由于记录的是 $j$ 及其之前的答案,所以也只需要前缀最大值即可。
最后倍增答案,判断是否合法即可。
时空复杂度 $O(n\log n)$。
Code:
#include<bits/stdc++.h>
using namespace std;
int n,k,ans=INT_MAX;
const int N=2e6+6;
int _R[N],sta[N],h,t;
int A[21][N],f[N],g[N];
void work(int*A,int*B){
for(int i=1,r=1,mx=0;i<=2*n;++i){
while(r<=A[i]+1&&r<=2*n)mx=max(mx,B[r++]);
A[i]=mx;
}
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>k;
for(int i=1;i<=k;++i){
int l,r;
cin>>l>>r;
if(l>r)r+=n;
_R[l]=max(_R[l],r);
_R[l+n]=max(_R[l],r+n);
}
for(int i=1;i<=2*n;++i)A[0][i]=max(A[0][i-1],_R[i]);
for(int i=1;i<21;++i){
memcpy(A[i],A[i-1],sizeof*A);
work(A[i],A[i-1]);
}
for(int i=1;i<=n;++i)f[i]=i;
int ans=0;
for(int i=20;~i;--i){
memcpy(g,f,sizeof g);
work(f,A[i]);
bool ok=0;
for(int j=1;j<=2*n&&!ok;++j)if(f[j]-j>=n)ok=1;
if(ok)memcpy(f,g,sizeof f);else ans|=1<<i;
}
if(++ans>1e6)cout<<"impossible";
else cout<<ans<<'\n';
return 0;
}
RE
题目大意:
给定一段长度为 $l$ 的文字,和一个 $n\times m$ 的网格图。网格图上每个格子为 . 或 X。
你需要从文字中选一段子串,然后选择网格图上的任意一个点 $(x,y)$ 作为起点。
要求:依次遍历选出的子串,遇到 l,r,u,d 字符时,分别使你当前所在的位置往左、右、上、下移动一格。并且恰好到达所有的 X 且不能到达 .(包括起点)。
问是否可行,如果可行输出你选的子串区间。
$l,n\times m\leq 10^5$。
题解:
我们先不管起点的位置,只需要满足你走到的点和图“形状相同”即可。
显然要完美覆盖这个图,经过的点的个数得和那张图上 X 的个数相等。
这样的子串区间显然有单调性。
我们用双指针维护当前选的子串区间,不断移动右指针直到走过的点的个数和 X 的个数相等,然后需要快速判断是否相等就好了。若合法则输出答案,否则左端点向右移继续当前过程。
那么问题在于如何快速判断是否相等。
我们可以取经过的点的最小的横、纵坐标作为基准(这个可以轻松使用 STL 在 $O(l\log l)$ 内维护),将点与图片对其。然后逐行判断即可。判断的时候可以采用 hash 的方式。
注意到 $nm\leq 10^5$,因此必然存在一维小于 $\sqrt{100000}$,我们枚举小的那一维判断即可。
时间复杂度 $O(l\log l+l\sqrt{nm})$。
Code:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int>PII;
const int N=2e5+5;
mt19937 mt(time(0)+(size_t)new char);
string s,A[N],tmp[N];
inline PII&operator+=(PII&a,const PII&b){
a.first+=b.first,a.second+=b.second;
return a;
}
int len,n,m;
PII ds[2004];
map<PII,int>tot;
int cnt;
char ch[N];
int k,pos[N];
multiset<int>hang,lie;
template<const int md>
struct Hasher{
int base,_[N];
Hasher(){
base=mt()%500000+100000;
for(int i=*_=1;i<=200000;++i)_[i]=(LL)_[i-1]*base%md;
}
inline int get(int wg){return _[wg];}
inline void upd(int&a){a+=a>>31&md;}
inline void add(int&a,int b){upd(a+=_[b]-md);}
inline void del(int&a,int b){upd(a-=_[b]);}
inline int shr(int a,int b){return(LL)a*_[b]%md;}
};
Hasher<1004535809>hx1;
Hasher<1000000009>hx2;
int _h1[N],_h2[N],P_h1[500],P_h2[500];
void work_picture(){
int LX=1e5,LY=1e5;
for(int i=0;i<n;++i)
for(int j=0;j<m;++j)if(A[i][j]=='X')LX=min(LX,i),LY=min(LY,j);
for(int i=LX;i<n;++i)
for(int j=LY;j<m;++j)
if(A[i][j]=='X')hx1.add(P_h1[i-LX],j-LY),hx2.add(P_h2[i-LX],j-LY);
}
int main(){
freopen("easy.in","r",stdin);
freopen("easy.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>len,getline(cin,s),getline(cin,s),cin>>n>>m;
s=" "+s;
for(int i=1;i<=len;++i)if(s[i]=='l'||s[i]=='r'||s[i]=='u'||s[i]=='d')
ch[++k]=s[i],pos[k]=i;
for(int i=0;i<n;++i)cin>>tmp[i];
int tot_pic=0;
for(int i=0;i<n;++i)for(char c:tmp[i])tot_pic+=c=='X';
ds['l']=make_pair(0,-1);
ds['r']=make_pair(0,1);
ds['u']=make_pair(-1,0);
ds['d']=make_pair(1,0);
if(n>m){
for(int i=0;i<n;++i)
for(int j=0;j<m;++j)A[j]+=tmp[i][j];
swap(ds['l'],ds['u']);
swap(ds['r'],ds['d']);
swap(n,m);
}else for(int i=0;i<n;++i)A[i]=tmp[i];
work_picture();
PII _begin=make_pair(100000,100000),_end=_begin;
++tot[_begin];
_h1[100000]=hx1.get(1e5);
_h2[100000]=hx2.get(1e5);
hang.insert(100000),lie.insert(100000);
cnt=1;
for(int i=1,_i=1;i<=k;++i){
_end+=ds[(int)ch[i]];
if(!tot[_end]++){
++cnt;
hx1.add(_h1[_end.first],_end.second);
hx2.add(_h2[_end.first],_end.second);
hang.insert(_end.first),lie.insert(_end.second);
}
if(cnt==tot_pic){
int lx=*hang.begin(),ly=*lie.begin();
bool ok=1;
for(int i=0;i<n&&ok;++i){
int h1=_h1[lx+i],h2=_h2[lx+i];
if(!(h1==hx1.shr(P_h1[i],ly)&&h2==hx2.shr(P_h2[i],ly)))ok=0;
}
if(ok){
cout<<"YES\n"<<pos[_i]<<' '<<pos[i]<<'\n';
return 0;
}
while(cnt==tot_pic){
if(!--tot[_begin]){
--cnt;
hx1.del(_h1[_begin.first],_begin.second);
hx2.del(_h2[_begin.first],_begin.second);
hang.erase(hang.find(_begin.first));
lie.erase(lie.find(_begin.second));
}
_begin+=ds[(int)ch[_i++]];
}
}
}
cout<<"NO\n";
return 0;
}
OJ
题目大意:
给定 $n$ 个点 $m$ 条边,边带权值 $w$,保证无重边。
有 $q$ 个询问,每次给出 $l,h$,要求你只能使用权值在 $[l,h]$ 的边,且让尽可能多的点连通,在此基础上使用到的边的边权最少。求最少边权。
多测,强制在线。
$1\leq n\leq 10^3$,$1\leq m\leq 10^5$,$1\leq q,w,l,h\leq 10^6$。
题解:
对每个询问,我们贪心地选择最小的边是最优的。这个过程同 Kruskal。加到不能加为止,用到的边的权值和就是最小的。
我们先不考虑上界,仅考虑下界。那么这就是一个经典的问题,可以用贪心求解。
将边权从大到小排序,按顺序把边插入。插入一条边的时候,若两点原来不连通,则直接添加。若两点原来连通,则一定形成了一个环,将环上边权最大的那条边删掉用新边替代即可。证明略。
可以用 LCT 来维护。时间复杂度 $O(m\log n)$。
那么现在有了上界的限制。我们只需要在只有下界限制求出的图中,将边权超过上界的边删掉即为答案。
原因:由贪心过程可知,若删掉那些边后,存在一条在范围内的边能使答案更优,则这条边一定能替换掉另一条边权比它大的边使只有下界时的答案更优。所以并不存在这样的边。
于是我们只需要在 LCT 的过程中,用权值线段树维护使用的边的边权和。查询时直接在线段树上区间查询即可。
由于本题强制在线,所以需要使用可持久化线段树。
时间复杂度 $O(m\log n+q\log m)$。空间复杂度 $O(m\log m)$。
Code:
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int N=2e5+6;
int n,m,q;
namespace lct{
int fa[N],ch[N][2],tag[N];
pair<int,int>mx[N],val[N];
inline int ckr(int x,const int p=1){return ch[fa[x]][p]==x;}
inline int isroot(int x){return!(ckr(x)||ckr(x,0));}
inline void flip(int x){std::swap(ch[x][0],ch[x][1]),tag[x]^=1;}
inline void update(int x){mx[x]=std::max(val[x],std::max(mx[ch[x][0]],mx[ch[x][1]]));}
inline void pushdown(int x){if(tag[x]){tag[x]=0;if(ch[x][0])flip(ch[x][0]);if(ch[x][1])flip(ch[x][1]);}}
inline void rotate(int x){
int y=fa[x],z=fa[y],k=ckr(x);
if(!isroot(y))ch[z][ckr(y)]=x;
fa[x]=z,fa[y]=x,fa[ch[x][!k]]=y;
ch[y][k]=ch[x][!k],ch[x][!k]=y;
update(y);
}
inline void splay(int x){
static int sta[N],top;sta[top=1]=x;
for(int y=x;!isroot(y);sta[++top]=y=fa[y]);
while(top)pushdown(sta[top--]);
for(;!isroot(x);rotate(x))
if(!isroot(fa[x]))rotate((ckr(x)^ckr(fa[x]))?x:fa[x]);
update(x);
}
inline void access(int x){for(int t=0;x;ch[x][1]=t,t=x,x=fa[x])splay(x);}
inline void makeroot(int x){access(x),splay(x),flip(x);}
inline void split(int x,int y){makeroot(x),access(y),splay(y);}
inline int findroot(int x){access(x);for(splay(x);ch[x][0];x=ch[x][0]);splay(x);return x;}
inline void link(int x,int y){makeroot(x),fa[x]=y;}
inline void cut(int x,int y){makeroot(x),access(y),splay(y),ch[y][0]=fa[x]=0,update(y);}
inline pair<int,int>query(int x,int y){split(x,y);return mx[y];}
inline int connect(int x,int y){return findroot(x)==findroot(y);}
}
namespace sgt{
LL sum[N*32];int ls[N*32],rs[N*32],nod;
void add(int&o,int pre,int l,int r,const int&pos,const int&v){
o=++nod,ls[o]=ls[pre],rs[o]=rs[pre],sum[o]=sum[pre]+v;
if(l<r){
const int mid=(l+r)/2;
if(pos<=mid)add(ls[o],ls[pre],l,mid,pos,v);
else add(rs[o],rs[pre],mid+1,r,pos,v);
}
}
LL query(int o,int l,int r,const int&L,const int&R){
if(!o)return 0;
if(L<=l&&r<=R)return sum[o];
LL res=0;
const int mid=(l+r)/2;
if(L<=mid)res=query(ls[o],l,mid,L,R);
if(mid<R)res+=query(rs[o],mid+1,r,L,R);
return res;
}
}
struct EDGE{
int u,v,w;
inline bool operator<(const EDGE&rhs)const{return w<rhs.w;}
}e[N];
int rt[N];
void addedge(int id,int&rt){
int u=e[id].u,v=e[id].v,w=e[id].w;
int pos=lower_bound(e+1,e+m+1,(EDGE){0,0,w})-e;
sgt::add(rt,rt,1,m,pos,w);
if(lct::connect(u,v)){
pair<int,int>dd=lct::query(u,v);
pos=lower_bound(e+1,e+m+1,(EDGE){0,0,dd.first})-e;
sgt::add(rt,rt,1,m,pos,-dd.first);
int uu=e[dd.second].u,vv=e[dd.second].v;
lct::cut(uu,dd.second+n),lct::cut(vv,dd.second+n);
}
lct::val[n+id]=lct::mx[n+id]=make_pair(w,id);
lct::link(u,n+id),lct::link(v,n+id);
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int T;
for(cin>>T;T--;){
cin>>n>>m;
for(int i=1;i<=m;++i)
cin>>e[i].u>>e[i].v>>e[i].w;
sort(e+1,e+m+1);
for(int i=m;i;--i)addedge(i,rt[i]=rt[i+1]);
for(int i=2;i<=m;++i)
if(e[i].w==e[i-1].w)rt[i]=rt[i-1];
cin>>q;
LL ans=0;
while(q--){
LL l,r;
cin>>l>>r;
l-=ans,r-=ans;
assert(1<=l&&l<=r&&r<=1000000);
int pos=lower_bound(e+1,e+m+1,(EDGE){0,0,(int)l})-e;
int R=upper_bound(e+1,e+m+1,(EDGE){0,0,(int)r})-e-1;
ans=sgt::query(rt[pos],1,m,1,R);
cout<<ans<<'\n';
}
for(int i=1;i<=n+m;++i)
lct::fa[i]=lct::ch[i][0]=lct::ch[i][1]=lct::tag[i]=0,
lct::mx[i]=lct::val[i]=make_pair(0,0);
for(int i=1;i<=m;++i)rt[i]=0;
sgt::nod=0;
}
return 0;
}
LI
题目大意:
给定一个长度为 $n$ 的排列 $p$。$m$ 次询问,每次询问给出 $x,y$,求包含 $p_x,p_y$ 的最短的值域连续段。输出两个端点。
题解:
析合树模板题。
建出析合树,每次询问的时候查询 $p_x$ 和 $p_y$ 在析合树上的 LCA。
若 LCA 为析点或 $x=y$,则 LCA 代表的这段区间就是答案。
若 LCA 为合点且 $x\neq y$,我们要找 LCA 的儿子中最短的包含 $p_x,p_y$ 的段。分别找到 $p_x,p_y$ 对应的儿子结点即可。
建析合树的过程使用较易理解的做法,时间复杂度 $O(n\log n)$,空间复杂度 $O(n)$。
有关析合树的参考资料:
Code:
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+6;
int n,p[N],m,psn[N];
namespace rmq{
int mn[N<<2],mx[N<<2];
void build(int l,int r,int o){
if(l==r)mn[o]=mx[o]=psn[l];else{
const int mid=(l+r)/2;
build(l,mid,o<<1),build(mid+1,r,o<<1|1);
mn[o]=min(mn[o<<1],mn[o<<1|1]);
mx[o]=max(mx[o<<1],mx[o<<1|1]);
}
}
int _min(const int&L,const int&R,int l=1,int r=n,int o=1){
if(L<=l&&r<=R)return mn[o];
const int mid=(l+r)/2;
int res=1e9;
if(L<=mid)res=_min(L,R,l,mid,o<<1);
if(mid<R)res=min(res,_min(L,R,mid+1,r,o<<1|1));
return res;
}
int _max(const int&L,const int&R,int l=1,int r=n,int o=1){
if(L<=l&&r<=R)return mx[o];
const int mid=(l+r)/2;
int res=0;
if(L<=mid)res=_max(L,R,l,mid,o<<1);
if(mid<R)res=max(res,_max(L,R,mid+1,r,o<<1|1));
return res;
}
void init(){build(1,n,1);}
}
namespace sgt{
pair<int,int>d[N<<2];
int tag[N<<2];
inline void pushdown(int o){
if(int&x=tag[o]){
d[o<<1].first+=x,d[o<<1|1].first+=x;
tag[o<<1]+=x,tag[o<<1|1]+=x;
x=0;
}
}
void add(int l,int r,int o,const int&L,const int&R,const int&v){
if(d[o].first>=1000000000)return;
if(L<=l&&r<=R){
d[o].first+=v;
tag[o]+=v;
}else{
pushdown(o);
const int mid=(l+r)/2;
if(L<=mid)add(l,mid,o<<1,L,R,v);
if(mid<R)add(mid+1,r,o<<1|1,L,R,v);
if(d[o<<1].first<d[o<<1|1].first)d[o]=d[o<<1];
else d[o]=d[o<<1|1];
}
}
void modify(int l,int r,int o,const int&pos,const pair<int,int>&v){
if(l==r)d[o]=v;else{
pushdown(o);
const int mid=(l+r)/2;
if(pos<=mid)modify(l,mid,o<<1,pos,v);
else modify(mid+1,r,o<<1|1,pos,v);
if(d[o<<1].first<d[o<<1|1].first)d[o]=d[o<<1];
else d[o]=d[o<<1|1];
}
}
}
namespace xht{
int head[N],cnt;
struct edge{
int to,nxt;
}e[N];
inline void addedge(int u,int v){e[++cnt]=(edge){v,head[u]},head[u]=cnt;}
struct node{
int l,r;
bool X;
inline int length(){return r-l;}
}a[N];
int nod,sta[N],top,tmax,tmin,rt;
pair<int,int>_max[N],_min[N];
void insert(int id){
int val=id;
if(!top){
sta[++top]=id;
sgt::modify(1,n,1,top,make_pair(0,top));
if(!tmax||_max[tmax].first!=a[id].r)_max[++tmax]=make_pair(a[id].r,top);
if(!tmin||_min[tmin].first!=a[id].l)_min[++tmin]=make_pair(a[id].l,top);
return;
}
while(top){
if(a[sta[top]].X&&max(a[sta[top]].r,a[id].r)-min(a[sta[top]].l,a[id].l)==a[sta[top]].length()+a[id].length()){
sgt::modify(1,n,1,top,make_pair(1000000000,0));
int x=sta[top--];
a[x].r=max(a[x].r,a[id].r),a[x].l=min(a[x].l,a[id].l);
addedge(x,id);
id=x;
}else break;
}
--sgt::tag[1],--sgt::d[1].first;
int pre=top;
while(tmax&&_max[tmax].first<val){
sgt::add(1,n,1,_max[tmax].second,pre,val-_max[tmax].first);
pre=_max[tmax].second-1;
--tmax;
}
if(pre<top)
_max[++tmax]=make_pair(val,pre+1);
pre=top;
while(tmin&&_min[tmin].first>val){
sgt::add(1,n,1,_min[tmin].second,pre,_min[tmin].first-val);
pre=_min[tmin].second-1;
--tmin;
}
if(pre<top)
_min[++tmin]=make_pair(val,pre+1);
while(top){
pair<int,int>zd=sgt::d[1];
if(zd.first)break;
if(zd.second==top&&a[sta[top]].X==0){
int x=sta[top];
if((psn[a[x].l]<psn[a[x].r]&&a[x].r<a[id].l)||(psn[a[x].l]>psn[a[x].r]&&a[x].r>a[id].l)){
sgt::modify(1,n,1,top,make_pair(1000000000,0));
addedge(x,id);
a[x].l=min(a[x].l,a[id].l);
a[x].r=max(a[x].r,a[id].r);
--top;
id=x;
continue;
}
}
int nw=++nod;
if(zd.second<top)a[nw].X=1;
a[nw].r=a[id].r,a[nw].l=a[id].l;
for(int i=zd.second;i<=top;++i){
sgt::modify(1,n,1,i,make_pair(1000000000,0));
a[nw].r=max(a[nw].r,a[sta[i]].r);
a[nw].l=min(a[nw].l,a[sta[i]].l);
addedge(nw,sta[i]);
}
addedge(nw,id);
top=zd.second-1;
id=nw;
}
while(tmax&&_max[tmax].second>top)--tmax;
while(tmin&&_min[tmin].second>top)--tmin;
sta[++top]=id;
sgt::modify(1,n,1,top,make_pair(0,top));
if(!tmax||_max[tmax].first!=a[id].r)_max[++tmax]=make_pair(a[id].r,top);
if(!tmin||_min[tmin].first!=a[id].l)_min[++tmin]=make_pair(a[id].l,top);
}
void build(){
nod=n;
for(int i=1;i<N<<2;++i)sgt::d[i]=make_pair(1000000000,0);
for(int i=1;i<=n;++i)a[i]=(node){i,i,0};
for(int i=1;i<=n;++i)
insert(p[i]);
rt=sta[1];
}
int fa[N],dep[N],Top[N],sz[N],son[N];
void dfs(int now){
sz[now]=1;
for(int i=head[now];i;i=e[i].nxt){
fa[e[i].to]=now,dep[e[i].to]=dep[now]+1;
dfs(e[i].to);
sz[now]+=sz[e[i].to];
if(!son[now]||sz[son[now]]<sz[e[i].to])
son[now]=e[i].to;
}
}
void dfs2(int now){
if(son[now])Top[son[now]]=Top[now],dfs2(son[now]);
for(int i=head[now];i;i=e[i].nxt)if(e[i].to!=son[now])
dfs2(Top[e[i].to]=e[i].to);
}
inline int LCA(int x,int y){
while(Top[x]!=Top[y])if(dep[Top[x]]>dep[Top[y]])x=fa[Top[x]];else y=fa[Top[y]];
return dep[x]<dep[y]?x:y;
}
inline int get(int u,int v){
while(Top[u]!=Top[v]){
if(fa[Top[v]]==u)return Top[v];
v=fa[Top[v]];
}
return son[u];
}
void init(){
dep[rt]=1;
dfs(rt),dfs2(Top[rt]=rt);
}
void query(int l,int r){
int t=LCA(l,r);
if(a[t].X||l==r){
cout<<rmq::_min(a[t].l,a[t].r)<<' '<<rmq::_max(a[t].l,a[t].r)<<'\n';
return;
}
int ls=get(t,l),rs=get(t,r);
int R=max(a[ls].r,a[rs].r),L=min(a[ls].l,a[rs].l);
cout<<rmq::_min(L,R)<<' '<<rmq::_max(L,R)<<'\n';
}
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;++i)cin>>p[i],psn[p[i]]=i;
rmq::init();
xht::build();
xht::init();
for(cin>>m;m--;){
int l,r;
cin>>l>>r;
xht::query(p[l],p[r]);
}
return 0;
}
FB
题目大意:
你要修一座拱桥。桥的高度为 $h$。给出 $n$ 个点 $(x_1,y_1),(x_2,y_2),\ldots,(x_n,y_n)$,将所有相邻两个点连起来就是地面。
你需要修若干条柱子,只能在给定的点对应的横坐标处修,在第 $i$ 个点处修的柱子的高度为 $h-x_i$。第 $1$ 个和第 $n$ 个点处必须修柱子。
你还需要在修的柱子之间造拱,拱是一个半圆形,直径为两个柱子的距离,恰好和桥面相切。
拱不能和地面相交,可以相切。
假设你修了 $k$ 条柱子,高度为 $h_1,h_2,\ldots,h_k$,其中 $k-1$ 个拱的直径为 $d_1,d_2,\ldots,d_{k-1}$。
给定参数 $\alpha,\beta$,要求最小化:
无合法方案输出 impossible。
$1\leq n\leq 10^4$。
题解:
考虑动态规划。
记 $f_i$ 表示点 $i$ 之前都修完了,且 $i$ 处修柱子的最小花费。
转移时枚举前一个柱子的位置 $j$,然后加上 $i$ 的柱子和 $i,j$ 之间的距离的贡献,取 $\min$ 即可。
由于题目有限制条件,因此要判断拱和每个点是否相交。加上判断的时间,复杂度为 $O(n^3)$。
我们对于点 $(a,b)$,拱的半径为 $r$,当前考虑建柱子的的点为 $(x,y)$,考虑拱和两个点不相交需要满足的条件。
两个最基本的条件是:$a+r>h$,$x+r>h$。
半圆圆心的位置为 $(x-r,h-r)$,则点 $(a,b)$ 在圆内或圆上必须满足:
记 $a_0=x-a,a_1=h-b$。
解一元二次方程可得到 $r_1,r_2$($r_1\le r_2$)。则当 $r_1\leq r\leq r_2$ 时,点在圆内或圆上。由于只要求点在半圆内或半圆上,因此当 $b<h-r_1$ 时不取 $r_1$ 的下界。
然后转移的时候维护当前 $r$ 的可选范围即可。
时间复杂度 $O(n^2)$。
Code:
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+6;
typedef long long LL;
int n,h,alpha,beta,X[N],Y[N];
LL d[N];
void solve(int a,int b,LL c,double&x1,double&x2){
LL dlt=(LL)b*b-4*a*c;
if(dlt<0){x1=1e11,x2=-1e11;}
double cd=sqrt(dlt);
x1=(-b+cd)/(2*a),x2=(-b-cd)/(2*a);
if(x1>x2)swap(x1,x2);
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>h>>alpha>>beta;
for(int i=1;i<=n;++i)
cin>>X[i]>>Y[i];
memset(d,0x3f,sizeof d);
d[1]=(LL)alpha*(h-Y[1]);
for(int i=2;i<=n;++i){
double l=0,r=1e12;
for(int j=i-1;j;--j){
int d=X[i]-X[j];
if(Y[i]*2+d>2*h)break;
int a1=X[i]-X[j],b1=h-Y[j];
double x1,x2;
solve(1,-2*(a1+b1),(LL)a1*a1+(LL)b1*b1,x1,x2);
if(x1-1e-5>x2)break;
if(h-x1<=Y[j])l=max(l,x1);
r=min(r,x2);
if(l-1e-5>r)break;
if(l*2-1e-5<=d&&d<=r*2+1e-5)
::d[i]=min(::d[i],::d[j]+(LL)alpha*(h-Y[i])+(LL)beta*d*d);
}
}
if(d[n]>1e17)cout<<"impossible\n";
else cout<<d[n]<<'\n';
return 0;
}
FG
题目大意:
给定一棵 $n+1$ 个结点的有根树,每条边上有字母。一个结点代表的字符串是这个结点到根的有向路径上经过的边权上的字母依次排列。
有 $k$ 个询问,每个询问给出字符串 $S$,问 $S$ 作为树上多少个结点代表的串的前缀。
$1\leq n,k,\sum |S|\leq 10^5$。
题解:
考虑把所有串都反过来,那么这棵给定的树就是一棵比较正常的字典树。然后,把询问串倒过来后,相当于询问 $S$ 作为一个串的后缀的出现次数。
对所有询问串建 AC 自动机,然后在 Trie 和 AC 自动机上同时 dfs,将 dfs 到的 AC 自动机上的结点的点权 $+1$。
一个结点代表的串作为后缀的出现次数,就是它在 fail 树上的子树的点权和。最后再 dfs 一遍求子树点权和即可。
时间复杂度 $O(n+k+26\sum |S|)$。
Code:
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+9;
int n,m,fa[N],head[N],aid[N],tot[N];
struct edge{
int to,nxt;char c;
}e[N];
queue<int>q;
int ch[N][26],fail[N],nod=0;
vector<int>G[N];
void insert(char*s,int id){
int nw=0;
for(int i=0;s[i];++i){
int c=s[i]-'A';
if(!ch[nw][c])ch[nw][c]=++nod;
nw=ch[nw][c];
}
aid[id]=nw;
}
void build(){
for(int i=0;i<26;++i)if(ch[0][i])q.push(ch[0][i]);
while(!q.empty()){
int u=q.front();q.pop();
for(int c=0;c<26;++c)if(ch[u][c]){
fail[ch[u][c]]=ch[fail[u]][c];
q.push(ch[u][c]);
}else ch[u][c]=ch[fail[u]][c];
}
}
void dfs(int now,int nw){
int _=nw;
++tot[_];
for(int i=head[now];i;i=e[i].nxt){
int c=e[i].c-'A';
nw=ch[_][c];
dfs(e[i].to,nw);
}
}
void DFS(int u){for(int i:G[u])DFS(i),tot[u]+=tot[i];}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;++i){
char s[8];
cin>>s>>fa[i];
e[i]=(edge){i,head[fa[i]],*s},head[fa[i]]=i;
}
for(int i=1;i<=m;++i){
static char s[N];
cin>>s;
reverse(s,s+strlen(s));
insert(s,i);
}
build();
dfs(0,0);
for(int i=1;i<=nod;++i)G[fail[i]].push_back(i);
DFS(0);
for(int i=1;i<=m;++i)cout<<tot[aid[i]]<<'\n';
return 0;
}
LL
题目大意:
给定二维平面 $n$ 个正方形,保证 $4$ 个顶点以及中点都在整点上。
正方形的边保证要么与坐标轴平行,要么与坐标轴夹角为 $45^\circ$。
求 $n$ 个正方形覆盖的部分的面积大小。
$1\leq n\leq 10^5$,$|x|,|y|,|d|\leq 1000$。
题解:
注意到坐标范围非常地小,因此我们可以直接差分前缀和。
将两类正方形分开处理比较方便。
对于 A 类(与坐标轴平行的),我们令 $A_{i,j}$ 表示左上角为 $(i,j)$ 的小正方形被覆盖的次数。这就是一个基本的二维差分/前缀和。
对于 B 类(不与坐标轴平行的),也可以类似处理。令 $B_{i,j}$ 表示 $(i,j),(i+1,j-1),(i+1,j+1),(i+2,j)$ 为顶点的正方形被覆盖的次数。这个也可以差分/前缀和处理:$B_{i,j}=B_{i,j}+B_{i-1,j-1}+B_{i-1,j+1}-B_{i-2,j}$。
在坐标范围平方的时间内处理即可。
Code:
#include<bits/stdc++.h>
using namespace std;
int n;
struct array{
int a[4005][4005];
inline int*operator[](const int&x){return a[x+2001]+2001;}
}A,B;
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
while(n--){
char tp[8];
int x,y,d;
cin>>tp>>x>>y>>d;
d/=2;
if(*tp<'B'){
++A[x-d][y-d],--A[x-d][y+d],--A[x+d][y-d],++A[x+d][y+d];
}else{
++B[x-d][y],--B[x][y-d],--B[x][y+d],++B[x+d][y];
}
}
for(int i=-1500;i<=1500;++i)
for(int j=-1500;j<=1500;++j){
A[i][j]+=A[i-1][j]+A[i][j-1]-A[i-1][j-1];
B[i][j]+=B[i-1][j-1]+B[i-1][j+1]-B[i-2][j];
}
int ans=0;
for(int i=-1500;i<=1500;++i)
for(int j=-1500;j<=1500;++j)
if(A[i][j])ans+=4;else{
if(B[i-1][j+1]||B[i][j+1])++ans;
if(B[i][j+1]||B[i][j])++ans;
if(B[i][j]||B[i-1][j])++ans;
if(B[i-1][j]||B[i-1][j+1])++ans;
}
printf("%.2f\n",ans/4.);
return 0;
}
QE
题目大意:
给定 $n$ 个正整数 $a_1,a_2,\dots,a_n$,你每次可以对一个数进行操作,使它乘上任意一个正整数。
对 $0\sim n$ 的每个整数 $k$,求出恰好进行 $k$ 次操作时,$n$ 个整数中不同的整数个数最少是多少。
$1\leq n\leq 3\times 10^5$,$1\leq a_i\leq 10^6$。
题解:
考虑如何让不同的整数个数减少。
有两种方式:
- 对于一个值的数,若原来的整数中存在它的 $2$ 倍及以上的倍数,则变成它的倍数,使整数个数减少 $1$。
- 找到 $a_1,a_2,\ldots,a_n$ 的任意一个公倍数,对于一些数,将它们都变成这个公倍数。
最开始做的时候我以为最优的做法是两种方法结合,即执行 1 操作一部分后再执行 2 操作。实际上,两种方法应该分开计算。
1 执行一段后再执行 2 的做法,我们可以把 1 执行的那一段也变成 2 的段,这样答案并不会变劣。
然后显然出现次数少的数优先执行操作。因此对出现次数排序计算即可。
Code:
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+7;
int n,a[N],tot[N];
vector<int>A,B;
bool vis[N];
int ans[N];
int main(){
freopen("equal.in","r",stdin);
freopen("equal.out","w",stdout);
memset(ans,0x3f,sizeof ans);*ans=0;
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;++i)cin>>a[i],++tot[a[i]],vis[a[i]]=1;
A.push_back(0),B.push_back(0);
for(int i=1;i<=1000000;++i)if(tot[i]){
A.push_back(tot[i]),++*ans;
for(int j=i+i;j<=1000000;j+=i)if(tot[j]){B.push_back(tot[i]);break;}
}
sort(A.begin(),A.end());
sort(B.begin(),B.end());
for(int i=1;i<(int)A.size();++i)A[i]+=A[i-1];
for(int i=1;i<(int)B.size();++i)B[i]+=B[i-1];
for(int i=1,it=0;i<=n;++i){
while(it+1<(int)A.size()&&A[it+1]<=i)++it;
ans[i]=min(ans[i],*ans-it+1);
}
for(int i=1,it=0;i<=n;++i){
while(it+1<(int)B.size()&&B[it+1]<=i)++it;
ans[i]=min(ans[i],*ans-it);
}
for(int i=1;i<=n;++i)ans[i]=min(ans[i],ans[i-1]);
for(int i=0;i<=n;++i)cout<<ans[i]<<' ';
return 0;
}
RJ
题目大意:
有一种语言,数的值域在 $0..255$ 之间。支持 + - * / min max 操作(除法为四舍五入,其他运算在模 $256$ 意义下进行)。
操作数只有 ?,每个 ? 都是一个独立的 $0..255$ 之间均匀随机的数。
支持宏定义 <mac> = <exp>,代码中所有 <mac> 都会被 (<exp>) 替代。
除了宏定义以外,你只能写一个该语言的表达式,它的运算结果将被输出。
给定 $c$,你需要给出一段除去空白字符后长度不超过 $256$ 的该语言的代码,使得代码的输出为 $c$ 的概率不小于 $\frac 1 2$。
题解:
$c=0$ 的情况样例已经给出,直接输出即可。
$c=1\sim 255$ 的情况不难想到按位处理。
我们将 $2^0,2^1,2^2,\ldots,2^7$ 用宏表示出来,然后就可以直接组成所有的 $c$。
那么我们需要准确地搞出这 $8$ 个数来。
我们考虑造一个 $1$。我们把很多的 ? 取最大值,让它有极高概率为 $255$,然后两个相除就是 $1$ 了。
剩下的 $2^i$ 可以由两个 $2^{i-1}$ 相加得到。
为了让弄出来的数尽可能多使得最大值为 $255$ 的概率接近 $1$,用多层宏定义的方式来做即可。
Code:
#include<bits/stdc++.h>
using namespace std;
int res;
const char s[]={'f','g','h','i','j','k','l','m'};
int main(){
freopen("java2016.in","r",stdin);
freopen("java2016.out","w",stdout);
scanf("%d",&res);
if(res==0)return puts("? / ? / ? / ?"),0;
puts("a = ? max ? max ? max ? max ? max ? max ? max ?");
puts("b = a max a max a max a max a max a max a max a");
puts("c = b max b max b max b max b max b max b max b");
puts("d = c max c max c max c max c max c max c max c");
puts("e = d / d");
puts("f = e max e max e max e max e max e max e max e");
puts("g = f + f");
puts("h = g + g");
puts("i = h + h");
puts("j = i + i");
puts("k = j + j");
puts("l = k + k");
puts("m = l + l");
string ans="";
for(int i=0;i<8;++i)if(res>>i&1)ans.push_back(s[i]),ans+=" + ";
ans.pop_back();
ans.pop_back();
ans.pop_back();
puts(ans.c_str());
return 0;
}
RG
题目大意:
给定一棵大小为 $n$ 的有根树。有 $q$ 个操作:
- 给定 $v$,将 $v$ 号结点上面加上一个强盗。保证之前没有。
- 给定 $v$,将 $v$ 号结点上面减去一个强盗。保证之前有。
你需要断掉最少的边,使所有强盗都不与根连通。在此基础上,你需要使没有强盗且不与根连通的叶结点最少。
每次操作完后,输出最少需要断掉的边,和在此基础上没有强盗且不与根连通的叶结点的最少个数。
$1\leq n,q\leq 10^5$。
题解:
数据范围小,可以使用树剖线段树。
考虑根的每个儿子的子树。显然每个儿子的子树里最多割掉一条边(割掉儿子到根的边是其中一种方案)。
割掉一条边,相当于割掉一棵子树,这棵子树必须得包含所有的强盗。
我们对每个强盗,将他所在结点到根路径上的点权都加一,那么如果有 $k$ 个强盗,必须割掉根的权值为 $k$ 的子树。由于权值不可能超过 $k$,所以就是点权的最大值。
不难发现权值恰好为 $k$ 的点一定是一条到根的路径。为了使包含的叶子尽可能少,我们要选最深的那个结点。所以第二关键字取结点深度或 dfs 序即可。
然后直接树剖线段树实现链加、子树最大值即可。
时间复杂度 $O(n+q\log^2 n)$。
Code:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+6;
int n,m,fa[N],sz[N],son[N],dfn[N],idx,dep[N],top[N],ts[N],idfn[N],head[N],leaf[N];
int _[N],es,_totqd,_sumsz;
pair<int,int>d[N<<2];
int tag[N<<2];
struct edge{
int to,nxt;
}e[N];
void dfs(int now,int&rt){
ts[now]=rt;
sz[now]=1,son[now]=0;
for(int i=head[now];i;i=e[i].nxt){
dep[e[i].to]=dep[now]+1;
dfs(e[i].to,rt);
sz[now]+=sz[e[i].to];
leaf[now]+=leaf[e[i].to];
if(!son[now]||sz[son[now]]<sz[e[i].to])
son[now]=e[i].to;
}
}
void dfs2(int now){
idfn[dfn[now]=++idx]=now;
if(son[now])top[son[now]]=top[now],dfs2(son[now]);
for(int i=head[now];i;i=e[i].nxt)if(e[i].to!=son[now])
dfs2(top[e[i].to]=e[i].to);
}
inline void pushdown(int o){
if(int&x=tag[o]){
d[o<<1].first+=x,d[o<<1|1].first+=x;
tag[o<<1]+=x,tag[o<<1|1]+=x;
x=0;
}
}
void build(int l,int r,int o){
if(l==r)d[o].second=l;else{
const int mid=(l+r)/2;
build(l,mid,o<<1),build(mid+1,r,o<<1|1);
d[o]=max(d[o<<1],d[o<<1|1]);
}
}
void modify(int l,int r,int o,const int&L,const int&R,const int&v){
if(L<=l&&r<=R)d[o].first+=v,tag[o]+=v;
else{
pushdown(o);
const int mid=(l+r)/2;
if(L<=mid)modify(l,mid,o<<1,L,R,v);
if(mid<R)modify(mid+1,r,o<<1|1,L,R,v);
d[o]=max(d[o<<1],d[o<<1|1]);
}
}
pair<int,int>query(int l,int r,int o,const int&L,const int&R){
if(L<=l&&r<=R)return d[o];
pushdown(o);
const int mid=(l+r)/2;
if(L<=mid&&mid<R)return max(query(l,mid,o<<1,L,R),query(mid+1,r,o<<1|1,L,R));
if(L<=mid)return query(l,mid,o<<1,L,R);
return query(mid+1,r,o<<1|1,L,R);
}
inline void add(int v,int x){
while(top[v]!=1)modify(1,n,1,dfn[top[v]],dfn[v],x),v=fa[top[v]];
modify(1,n,1,1,dfn[v],x);
}
int main(){
freopen("gangsters.in","r",stdin);
freopen("gangsters.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=2;i<=n;++i){
cin>>fa[i];
e[i]=(edge){i,head[fa[i]]},head[fa[i]]=i;
}
for(int i=1;i<=n;++i)leaf[i]=!head[i];
dep[1]=1;
sz[1]=n;
for(int i=head[1];i;i=e[i].nxt){
dep[e[i].to]=2;
dfs(e[i].to,e[i].to);
if(!son[1]||sz[son[1]<sz[e[i].to]])son[1]=e[i].to;
leaf[1]+=leaf[e[i].to];
}
dfs2(top[1]=1);
build(1,n,1);
while(m--){
char op[8];int v;
cin>>op>>v;
if(*op=='+'){
int tr=ts[v];
if(!_[tr])++es;else _sumsz-=leaf[_[tr]];
add(v,1);
pair<int,int>x=query(1,n,1,dfn[tr],dfn[tr]+sz[tr]-1);
_[tr]=idfn[x.second];
_sumsz+=leaf[_[tr]];
if(leaf[v]==1)++_totqd;
}else{
int tr=ts[v];
_sumsz-=leaf[_[tr]];
add(v,-1);
pair<int,int>x=query(1,n,1,dfn[tr],dfn[tr]+sz[tr]-1);
_[tr]=idfn[x.second];
if(x.first==0)_[tr]=0,--es;
else _sumsz+=leaf[_[tr]];
if(leaf[v]==1)--_totqd;
}
cout<<es<<' '<<_sumsz-_totqd<<'\n';
}
return 0;
}
CK
题目大意:
定义:
由一对单引号中间有一些不带引号的文字组成的串为一级串。
左右各有 $k$ 个单引号,中间为若干 $k-1$ 级串和不带单引号的文字拼接而成的字符串为 $k$ 级串。
例如 ''All 'work' and no 'play''' 是一个 $2$ 级串。
现在文字消失了,只留下一些引号,并且有一些引号中间的空不见了。
给定 $n$ 段引号的个数 $a_1,a_2,\ldots,a_n$,问这段引号原来最大能是几级串。无解输出 no quotation。
$k$ 个引号可以拆成 $a$ 个引号和 $(k-a)$ 个引号,可以继续拆分。但是两段引号不能拼接起来。
$1\leq n,a_i\leq 100$。
题解:
首先,引号个数之和必定是偶数,否则显然无解。
其次,不难发现,$k$ 级引号的最左边必然有 $k,k-1,k-2,\ldots,1$ 个引号,最右边必然有 $1,2,3,\ldots,k$ 个引号。
这样中间还有偶数个引号。
那么一个非常简单的构造方案就是:中间这些全都是 $1$ 级串。由于中间有偶数个引号,因此一定可行。
所以只需要枚举答案,判断前缀、后缀是否满足条件即可。
特判答案为 $1$ 的情况。
Code:
#include<bits/stdc++.h>
using namespace std;
int n,a[105],sum,b[105];
bool check(int*A,int x){
int it=1,p=A[1];
for(int i=x;i;--i){
if(p<i)return 0;
if(p>i)p-=i;else p=A[++it];
}
return 1;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i)scanf("%d",a+i),sum+=a[i];
memcpy(b,a,sizeof a);
reverse(b+1,b+n+1);
if(sum&1)return puts("no quotation"),0;
if(sum==2)return puts("1"),0;
int ans=-1;
for(int i=2;;++i){
int x=(i+1)*i;
if(x>sum)break;
if(check(a,i)&&check(b,i))ans=i;
}
if(ans==-1)puts("no quotation");else printf("%d\n",ans);
return 0;
}
KH
题目大意:
给定一个长度为 $n$ 的序列 $a$,问有多少子区间的 and 和与 xor 和相等。
$1\leq n\leq10^5$,$0\leq a_i\lt 2^{31}$。
题解:
枚举左端点 $l$。对每个二进制位考虑。我们找到这个二进制位在右边第一次为 $0$ 的位置 $k$,则对于 $r\in[l,k-1]$,$[l,r]$ 的 and 和的这一位一定为 $1$。而对于 $r\in[k,n]$,$[l,r]$ 的 and 和的这一位一定为 $0$。
因此对于一个左端点,区间 and 和的不同取值只有 $\log a$ 种,且每种。我们只需要从大到下枚举左端点,同时维护每个二进制位的 $0$ 的最左边出现位置即可。
对于 xor 和,我们记录前缀 xor 和,然后相当于在 $\log a$ 个区间里查询某个数的出现次数。直接二分即可。
时间复杂度 $O(n\log n\log a)$。
Code:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e5+5;
int n,a[N],b[N],W[32];
map<int,vector<int> >mp;
pair<int,int>pr[32];
LL ans;
int calc(int w,int l,int r){
if(l>r||!mp.count(w))return 0;
vector<int>&vc=mp[w];
return upper_bound(vc.begin(),vc.end(),r)-lower_bound(vc.begin(),vc.end(),l);
}
int main(){
freopen("hack.in","r",stdin);
freopen("hack.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;++i)cin>>a[i];
for(int i=n;i;--i)b[i]=b[i+1]^a[i];
for(int i=1;i<=n;++i){
mp[b[i]].push_back(i);
for(int j=0;j<31;++j)if(!(a[i]>>j&1))W[j]=i;
for(int j=0;j<31;++j)pr[j]=make_pair(W[j],j);
sort(pr,pr+31);
int nt=2147483647,nr=i;
for(int j=30;~j;--j){
ans+=calc(nt^b[i+1],pr[j].first+1,nr);
nr=pr[j].first;
if(!nr)break;
nt^=1<<pr[j].second;
}
if(nr)ans+=calc(nt^b[i+1],1,nr);
}
cout<<ans<<'\n';
return 0;
}
IK
题目大意:
给定一个 $n$ 个点 $m$ 条边的有向图。
要求找到一条 $1$ 出发回到 $1$ 的经过每个其他点各 $1$ 次,经过 $n$ 条边的路径。
$2\leq n\leq 10^5$,$0\leq m\leq n+20$。
题解:
若 $m<n$ 则显然无解。
令 $k=m-n$。
考虑到只有最多 $20$ 条非环边,相关的有 $40$ 个不同的点。那么其他的点的入度和出度必然都为 $1$。
我们把这些点和相关的边缩起来,则最多剩下 $2k$ 个点和 $2k$ 条边。
爆搜即可。分析一下复杂度应该是 $O(2^kk)$。实际运行时效率很高。
Code:
#include<bits/stdc++.h>
const int N=100022;
using namespace std;
const char*tok="There is no route, Karl!";
vector<int>G[N],_G[N];
vector<int>e_id[N];
int n,m,id,dg1[N],dg2[N],rot;
int city[N],_id[N];
bool vis[N],Key[N];
void output(){
for(int i=0;i<n;++i)
cout<<city[i]<<' ';
cout<<1<<'\n';
exit(0);
}
void dfs(int now,int num){
if(vis[now]){
if(num==n&&now==1)output();
return;
}
city[num]=now;
vis[now]=1;
for(int i:G[now])dfs(i,num+1);
}
void init(){
for(int i=1;i<=n;++i)if(dg1[i]>1||dg2[i]>1)Key[i]=1;
for(int x=1;x<=n;++x)if(Key[x]){
for(int to:G[x]){
++id;
int nw=to;
e_id[id].push_back(nw);
while(!Key[nw]){
nw=G[nw][0];
e_id[id].push_back(nw);
}
if(nw!=x)_G[x].push_back(id);
}
}
}
void _(int t){
static vector<int>ans;
for(int i=0;i<t;++i)
for(int to:e_id[_id[i]])ans.push_back(to);
int pos=-1;
for(int i=0;i<(int)ans.size()&&pos==-1;++i)
if(ans[i]==1)pos=i;
if(pos==-1)exit(1);
for(int i=pos;i<(int)ans.size();++i)cout<<ans[i]<<' ';
for(int i=0;i<pos;++i)cout<<ans[i]<<' ';
cout<<"1\n";
exit(0);
}
void DFS(int now,int top,int tot){
if(vis[now]){
if(tot==n&&now==rot)_(top);
return;
}
vis[now]=1;
for(int num:_G[now]){
int to=e_id[num].back();
_id[top]=num;
DFS(to,top+1,tot+(int)e_id[num].size());
}
vis[now]=0;
}
int main(){
freopen("king.in","r",stdin);
freopen("king.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m;
if(n>m)return cout<<tok<<'\n',0;
while(m--){
int u,v;
cin>>u>>v;
if(u==v)continue;
G[u].push_back(v);
++dg1[u],++dg2[v];
}
for(int i=1;i<=n;++i)if(!dg1[i]||!dg2[i]){
cout<<tok<<'\n';
return 0;
}
dfs(1,0);
init();
memset(vis,0,sizeof vis);
for(int i=1;i<=n;++i)if(Key[i]){rot=i,DFS(i,0,0);break;}
cout<<tok<<'\n';
return 0;
}
RI
题目大意:
给定 $n$ 个整点围成的凸多边形。求有多少条对角线将凸多边形分成两块面积均为整数的部分。
$3\leq n\le 2\times 10^5$。
题解:
一步简单的转化:求有多少条对角线将凸多边形分成两块面积的两倍均为偶数的部分。
如果凸多边形的面积的两倍是奇数,则显然无解。所以我们只需要考虑被分割的其中一块的面积的两倍的奇偶性。
我们先固定一个端点 $A$,并求出所有对角线 $A,B$ 分割出的面积的两倍的奇偶性情况。
然后按顺序枚举 $A$,考虑 $A$ 变成 $C$(存在边 $A,C$)时,其他点作为另一个端点时的奇偶性情况。
当 $(A,B)$ 变为 $(C,B)$ 时,其面积的两倍的变化量为 $\vec{BA}\times\vec{BC}$。
将其展开。
考虑它的奇偶性。
发现对于 $A,C$,我们只需要关心每个 $B$ 的两个坐标的奇偶性,就可以知道它们的面积的两倍的奇偶性是否发生了改变。
而 $B$ 两个坐标的奇偶性的不同情况只有 $4$ 种,对其分别记录总个数、当前个数。那么奇偶性翻转时只需要将当前个数改成总个数减去当前个数即可。
时间复杂度 $O(n)$。
Code:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=2e5+50;
struct point{
int x,y;
inline point operator-(const point&rhs)const{return(point){x-rhs.x,y-rhs.y};}
}a[N];
inline LL cross(const point&a,const point&b){
return(LL)a.x*b.y-(LL)a.y*b.x;
}
int n,zt[N],in[4],ct[4];
LL ans;
inline void flip(int x){
in[x]=ct[x]-in[x];
}
int main(){
freopen("integral.in","r",stdin);
freopen("integral.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;++i)cin>>a[i].x>>a[i].y;
int cur=0;
for(int i=1;i<=n;++i){
int s=(a[i].x&1)<<1|(a[i].y&1);
zt[i]=s;
++ct[s];
}
++in[zt[1]];
for(int i=2;i<=n;++i){
LL res=cross(a[i]-a[1],a[i-1]-a[1]);
cur^=res&1;
if(!cur)++in[zt[i]];
}
if(cur){
cout<<0<<'\n';
return 0;
}
ans+=in[0]+in[1]+in[2]+in[3]-3;
for(int i=2;i<=n;++i){
if(cross(a[i],a[i-1])&1)flip(0),flip(1),flip(2),flip(3);
if((a[i].x+a[i-1].x)&1)flip(1),flip(3);
if((a[i].y+a[i-1].y)&1)flip(2),flip(3);
ans+=in[0]+in[1]+in[2]+in[3]-3;
}
cout<<ans/2<<'\n';
return 0;
}
GJ
题目大意:
给定 $n$ 个点 $m$ 条边的带权无向图(权值为正)。你要从 $1$ 出发到 $n$,对于每一种走法,它的代价是经过的所有边中最大的 $k$ 条边的边权和(不足 $k$ 条则为全部)。求最小代价。
$n,m\leq 3000$,$1\leq k\lt n$。
题解:
对于不到 $k$ 条的我们可以直接跑最短路。
我们考虑枚举边权 $v$,并钦定它是第 $k$ 大的边权。对于原图上的每条边 $(u,v,w)$,我们将它的权值变为 $\max(0,w-v)$。然后跑最短路,并尝试用 $(\mathrm{dist}(1,n)+k\cdot v)$ 更新答案。
正确性说明:
除去不到 $k$ 条边的情况,最优答案一定只计算恰好 $k$ 条边的代价。
对于一个 $v$,若它的最短路中实际应该计算代价的边超过 $k$ 条,则会多统计一些边的权值。因此增大 $v$ 一定有更优的答案。
剩下的情况就是恰好 $k$ 条的情况。由于我们取的是最小值,因此就是最优解。
时间复杂度 $O(m^2\log n)$。
Code:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=3005;
struct edge{
int to,nxt,w;
}e[N*2];
struct data{
int u;LL d;
inline bool operator<(const data&rhs)const{return d>rhs.d;}
};
std::priority_queue<data>q;
int n,m,k,head[N],S,T;
LL ans=0x3fffffffffffffff;
LL dis[N];
bool vis[N];
void spfa(int wt){
memset(vis,0,sizeof vis);
memset(dis,0x3f,sizeof dis);
dis[S]=0;
for(q.push((data){S,dis[S]});!q.empty();){
int u=q.top().u;q.pop();
if(vis[u])continue;
vis[u]=1;
for(int i=head[u];i;i=e[i].nxt){
LL dt=dis[u]+max(0,e[i].w-wt);
if(dt<dis[e[i].to])dis[e[i].to]=dt,q.push((data){e[i].to,dt});
}
}
ans=min(ans,dis[T]+k*(LL)wt);
}
int main(){
scanf("%d%d%d",&n,&m,&k);
int cnt=0;
S=1,T=n;
for(int i=1;i<=m;++i){
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
e[++cnt]=(edge){v,head[u],w},head[u]=cnt;
e[++cnt]=(edge){u,head[v],w},head[v]=cnt;
}
spfa(0);
for(int i=1;i<=2*m;i+=2)spfa(e[i].w);
printf("%lld\n",ans);
return 0;
}
TF
题目大意:
给定一个长度为 $n$ 的序列 $a_1,a_2,a_3,\ldots,a_n$,求至少将其分成多少个连续段,满足这些连续段通过重排后依次拼接,能够使 $a_i$ 单调不下降。
$1\leq n\leq 10^5$。
题解:
对 $a_i$ 进行离散化,设序列为 $a_i’$,得到序列中不同的数有 $m$ 种。那么重排后 $a_i’$ 的顺序一定是 $1$ 到 $m$。
我们考虑将连续的相同元素划到一个段中,它们在答案中一定相邻,否则必然可以通过将它们放到相邻位置使答案变优。
假设有 $k$ 个这样的连续段。我们需要让连续段个数尽可能小,所以相当于最大化最终序列中位置相邻的连续段个数。
枚举 $a_i’$ 的取值。不难发现,这个取值的所有连续段中,只有放在开头的和结尾的两个段才可能和其他段拼成一个连续段。
不妨令 $f_i$ 表示段 $i$ 作为这个取值的开头时,能在 $k$ 个连续段基础上减少最多的连续段个数。令 $g_i$ 表示段 $i$ 作为这个取值的结尾时,能在 $k$ 个连续段基础上减少最多的连续段个数。
$f_i$ 有两种转移:一是直接拼在上一种取值的最大的 $g_j$ 后面($f_i=\max\{g_j\}$);另一种是拼在它前面那段的后面,并多减少一个($f_i=g_{i-1}+1$)必须满足段 $i-1$ 的取值恰好比段 $i$ 的取值小 $1$ 才能转移。
若不存在与 $i$ 同取值的其它段,则 $g_i=f_i$。否则若 $i$ 不是 $f$ 中最大的,则 $g_i$ 直接从 $f$ 中的最大值转移过来;反之则从次大值转移过来。
最后分成的最小段数就是 $(k-\max\{g_i\})$。
考虑输出答案。我们对于每个段作为取值的开头,记录最优情况下上一个段的编号;对于每个段作为取值的结尾,记录最优情况下当前取值的开头段的编号。然后倒推可以得到所有取值的开头和结尾段的编号。中间的随便怎么排都行。
然后根据最终序列,不难推出原序列的分段情况。
时间复杂度 $O(n\log n)$(sort) 或 $O(n)$(计数排序)。
Code:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,a[N],b[N],mdf[N],m,mx[N],dp[N],pre[N],ans,pid[N],dip[N],qwq[N];
bool vis[N];
vector<int>pos[N];
int main(){
freopen("fragmentation.in","r",stdin);
freopen("fragmentation.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;++i)cin>>a[i],b[i]=a[i];
sort(b+1,b+n+1);
mdf[b[1]]=++m;
for(int i=2;i<=n;++i)
if(mdf[b[i]]!=mdf[b[i-1]])mdf[b[i]]=++m;
for(int i=1;i<=n;++i)a[i]=mdf[a[i]];
ans=1;
pos[a[1]].push_back(1);
vis[1]=1;
int pr=1;
for(int i=2;i<=n;++i)if(a[i]!=a[i-1])
pos[a[i]].push_back(i),pre[i]=pr,pr=i,++ans,vis[i]=1;
for(int i:pos[1])dp[i]=0;
mx[1]=0;
if(pos[1].size()==1u)pid[pos[1][0]]=pos[1][0];else
for(int i:pos[1]){
if(i!=pos[1][0])pid[i]=pos[1][0];
else pid[i]=pos[1][1];
}
qwq[1]=pos[1][0];
if(m==1)
cout<<1<<'\n'<<n<<'\n';
for(int x=2;x<=m;++x){
int mx1=-1,id1=0,mx2=-1,id2=0;
for(int i:pos[x]){
int dlt=mx[x-1];
dip[i]=qwq[x-1];
if(a[pre[i]]==x-1&&dp[pre[i]]+1>dlt){
dlt=dp[pre[i]]+1,dip[i]=pre[i];
}
if(dlt>mx1)mx2=mx1,id2=id1,mx1=dlt,id1=i;
else if(dlt>mx2)mx2=dlt,id2=i;
}
if(pos[x].size()==1u)dp[pos[x][0]]=mx1,pid[id1]=id1;else
for(int i:pos[x])if(i==id1)dp[i]=mx2,pid[i]=id2;else dp[i]=mx1,pid[i]=id1;
mx[x]=mx1,qwq[x]=id2?id2:id1;
if(x==m){
cout<<ans-mx1<<'\n';
vector<int>vc;
for(int i=id2?id2:id1;pid[i];i=dip[pid[i]]){
int pre=pid[i];
if(pre==i)vc.push_back(pre);else{
vc.push_back(i);
for(int j:pos[a[i]])if(j!=i&&j!=pre)
vc.push_back(j);
vc.push_back(pre);
}
}
vector<int>vec;
reverse(vc.begin(),vc.end());
for(int i:vc){
vec.push_back(i);
for(int j=i+1;j<=n&&!vis[j];++j)vec.push_back(j);
}
vc=vec;
vector<pair<int,int> >out;
int len=1,beg=vc[0];
for(int i=1;i<(int)vc.size();++i)if(vc[i]==vc[i-1]+1)++len;
else{
out.emplace_back(beg,len);
len=1,beg=vc[i];
}
out.emplace_back(beg,len);
sort(out.begin(),out.end());
for(auto i:out)cout<<i.second<<' ';
break;
}
}
return 0;
}
BL
题目大意:
有 $n$ 天,每天有 $4$ 种可能的不同天气。每天是每种天气的概率分别是 $a,b,c,d$。
那么最终有 $4^n$ 种不同的序列。要求给这 $4^n$ 种不同的序列编上二进制编码,使得任意一个不是另一个的前缀。
求每个序列的最短期望长度。
题解:
最优编码方式就是哈夫曼编码。哈夫曼编码依据字符出现概率构造,满足“任意一个不是另一个的前缀”且“平均长度最短”。
其构造方式是:每次选两个概率最小的点,将它们连到新的节点上,并删掉,加入新的节点。新的节点概率为原来两个节点的概率之和。
显然可以使用堆来模拟。
对于本题,我们直接计算出每种情况下的概率,然后用堆模拟即可。时间复杂度 $O(4^nn)$。
这一看就不靠谱。
不难发现这些序列中,组成不同的只有 $O(n^3)$ 种。因此我们枚举每种天气的出现次数,并将相同的压在一个节点里存储。用堆模拟时,对于很多相同的节点,可以同时完成合并。
至于计算期望,每次增加一个点的时候,期望长度就增加两个原来的节点的概率之和。容易计算。
Code:
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b)for(int i=(a);i<=(b);++i)
typedef long long LL;
double a,b,c,d,ans;
int n;
LL fac[21];
struct data{
double g;LL d;
inline bool operator<(const data&rhs)const{return g>rhs.g;}
};
priority_queue<data>q;
int main(){
scanf("%d%lf%lf%lf%lf",&n,&a,&b,&c,&d);
for(int i=*fac=1;i<=n;++i)fac[i]=i*fac[i-1];
rep(A,0,n)rep(B,0,n-A)rep(C,0,n-A-B){
int D=n-A-B-C;
double g=pow(a,A)*pow(b,B)*pow(c,C)*pow(d,D);
LL t=fac[n]/fac[A]/fac[B]/fac[C]/fac[D];
ans+=g*t;
q.push((data){g,t});
}
while(q.size()){
data u=q.top();q.pop();
if(q.empty()&&u.d==1)break;
if(u.d>1){
LL k=u.d/2;
ans+=k*2*u.g;
q.push((data){u.g*2,k});
u.d-=k*2;
if(!u.d)continue;
}
data v=q.top();q.pop();
ans+=u.g+v.g,--v.d;
q.push((data){u.g+v.g,1});
if(v.d)q.push(v);
}
printf("%.10f\n",ans-1);
return 0;
}
QF
题目大意:
定义一种语言,它有 for 语句。其格式如下:
for <variable> in range(<from>, <to>):
<body>
该语句会将变量 <variable>从 <from> 迭代到 <to>,每次迭代执行 <body> 中的语句。
若 <from> 大于 <to> 则不会执行 <body>。
<from> 可以是变量或 $1$,<to> 可以是变量或 $n$。变量必须之前出现过。
现在给定若干层这样的 for 语句的嵌套,最内层语句为 lag。
定义 $f(n)$ 表示 lag 的执行次数。要求找到 $C,k$ 使得 $C\cdot n^k$ 是程序的渐进复杂度,即满足:
题解:
考虑 for i in range(a,b): 语句,它规定了 $a\leq i$ 以及 $i\leq b$。
对于 $a\leq b$ 的条件,我们由 $a$ 向 $b$ 连出有向边。如果图上有强连通分量,则这个强连通分量中的点的取值必须相同。
我们将图进行缩点,得到一张 DAG。这张 DAG 中的每个点都是可以在限制范围内任意取值的。因此题目中的 $k$ 就是 DAG 的点数。
对于常数项 $C$,我们只需要知道 DAG 上的 $m$ 个点有多少种不同的大小关系(即图的拓扑序个数),然后除以 $m!$ 即可。
求拓扑序个数可以使用状压 DP。
Code:
#include<bits/stdc++.h>
using namespace std;
const int N=21;
int n;
int id[127],nd=0;
int cnc[N][N],fa[N],e[N],ie[N],ID[N];
long long dp[1<<20];
vector<int>G[N];
inline int find(int x){while(x!=fa[x])x=fa[x]=fa[fa[x]];return x;}
int main(){
freopen("fygon20.in","r",stdin);
freopen("fygon20.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;--n;
string s;
getline(cin,s);
for(int i=1;i<=n;++i){
cin>>s;
getline(cin,s);
int c=s[1],l=s[12],r=s[15];
id[c]=nd;
if(l!='1')
G[id[l]].push_back(nd);
if(r!='n')
G[nd].push_back(id[r]);
++nd;
}
getline(cin,s);
for(int i=0;i<n;++i)for(int t:G[i])
cnc[i][t]=1;
for(int k=0;k<n;++k)
for(int i=0;i<n;++i)
for(int j=0;j<n;++j)
cnc[i][j]|=cnc[i][k]&&cnc[k][j];
for(int i=0;i<n;++i)fa[i]=i;
for(int i=0;i<n;++i)
for(int j=i+1;j<n;++j)
if(cnc[i][j]&&cnc[j][i]){
int x=find(i),y=find(j);
if(x!=y)fa[y]=x;
}
nd=0;
for(int i=0;i<n;++i)if(find(i)==i)ID[i]=nd++;
for(int x=0;x<n;++x){
int s=ID[find(x)];
for(int to:G[x]){
int t=ID[find(to)];
if(s!=t)
e[s]|=1<<t,ie[t]|=1<<s;
}
}
const int C=(1<<nd)-1;
*dp=1;
for(int S=1;S<=C;++S){
for(int t=0;t<nd;++t)
if((S>>t&1)&&(S&ie[t])==ie[t])
dp[S]+=dp[S^(1<<t)];
}
long long p=1,q=dp[C];
for(int i=2;i<=nd;++i)p*=i;
long long r=__gcd(p,q);
p/=r,q/=r;
cout<<nd<<' '<<q<<'/'<<p<<'\n';
return 0;
}
UJ
题目大意:
给定大小为 $N$ 的向量 $X$。
定义一种 J 语言,有以下几种运算:
- 双目运算(
+ - *):标量与标量运算,结果就是运算结果;向量与标量运算,相当于向量的每一分量与标量运算;向量与向量运算,即对应分量的运算。运算与符号对应的四则运算相同。 - 单目运算(
- *:):取反和平方(对向量的运算施加到所有分量上)。 - 仅针对向量的单目运算(
+/):将向量变为一个标量,结果为向量的各分量之和。
J 语言只包含这些运算符以及标量 $N$,向量 $X$,且所有运算都从右到左。
现在给你一个结果为标量的 J 语言表达式。输出运算结果对 $10^9$ 取模的值。
本题定义了表达式的 complexity:
- 标量的
complexity为 $0$。 - 向量的
complexity为 $1$。 - 加法运算和减法运算的
complexity是,所有参与该运算的表达式的complexity的最大值。 - 乘法的复杂度是,所有参与该运算的表达式的
complexity的和。 - 单目平方的复杂度是,参与该运算的表达式的
complexity的两倍。
保证表达式的所有子表达式的 complexity 不超过 $10$。
题解:
我们维护一个关于 $X$ 的多项式,将标量认为是多项式的常数项。
发现所有运算都相当于多项式的运算。
因此处理出 $X$ 的若干次方的信息,然后表达式计算的时候维护多项式的系数即可。由 complexity 的大小保证了算法的时间复杂度。
由于从右到左运算,因此可以用栈大力模拟。
Code:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int md=1e9;
vector<int>X[20];
int n,sum[20];
string expr;
struct data{
int type;
string token;
};
struct stk{
int tp;
vector<int>A;
};
vector<data>dc;
vector<stk>sk;
void init(){
for(int i=2;i<20;++i){
X[i].resize(n);
for(int x=0;x<n;++x)
X[i][x]=(LL)X[i-1][x]*X[1][x]%md,sum[i]=(sum[i]+X[i][x])%md;
}
}
inline int gettype(char c){
switch(c){
case'(':case')':case'+':case'-':case'*':case'/':case':':
return 1;
case'X':case'N':return 2;
}
if(isdigit(c))return 3;
return -1;
}
void work(){
for(int i=0;i<(int)expr.length();++i){
int tp=gettype(expr[i]);
if(tp==1){
string tk=string(1,expr[i]);
if(expr[i]=='-'){
if(dc.empty()||(dc.back().type==1&&dc.back().token!=")"))
tk="$"+tk;
}else
if(i+1<(int)expr.length()){
if(expr[i]=='+'&&expr[i+1]=='/')
tk.push_back(expr[++i]);
else if(expr[i]=='*'&&expr[i+1]==':')
tk.push_back(expr[++i]);
}
dc.push_back((data){1,tk});
}else if(tp==3){
string tk=string(1,expr[i]);
while(i+1<(int)expr.length()&&gettype(expr[i+1])==3)
tk.push_back(expr[++i]);
dc.push_back((data){3,tk});
}else{
dc.push_back((data){2,string(1,expr[i])});
}
}
}
void SQR(vector<int>&v){
vector<int>tmp(2*(int)v.size()-1);
for(int i=0;i<(int)v.size();++i)
for(int j=0;j<(int)v.size();++j)
tmp[i+j]=(tmp[i+j]+(LL)v[i]*v[j])%md;
v=tmp;
}
void FOLD(vector<int>&v){
int res=0;
for(int i=0;i<(int)v.size();++i)
res=(res+(LL)sum[i]*v[i])%md;
v.resize(1);
v[0]=res;
}
void ADD(vector<int>&a,vector<int>b){
int sz=(int)max(a.size(),b.size());
a.resize(sz),b.resize(sz);
for(int i=0;i<sz;++i)a[i]=(a[i]+b[i])%md;
}
void DEL(vector<int>&a,vector<int>b){
int sz=(int)max(a.size(),b.size());
a.resize(sz),b.resize(sz);
for(int i=0;i<sz;++i)a[i]=(a[i]-b[i]+md)%md;
}
void MUL(vector<int>&a,vector<int>b){
int sz=(int)a.size()+(int)b.size()-1;
vector<int>tmp(sz);
for(int i=0;i<(int)a.size();++i)
for(int j=0;j<(int)b.size();++j)
tmp[i+j]=(tmp[i+j]+(LL)a[i]*b[j])%md;
a=tmp;
}
void push_back(stk k){
while(1){
if(sk.empty()||sk.back().tp==5)break;
if(sk.back().tp==1){
cerr<<"RE"<<'\n';
exit(0);
}
int tp=sk.back().tp;sk.pop_back();
if(sk.empty()||sk.back().tp!=1){
cerr<<"RE"<<'\n';
exit(0);
}
stk tmp=sk.back();sk.pop_back();
switch(tp){
case 2:ADD(k.A,tmp.A);break;
case 3:DEL(k.A,tmp.A);break;
case 4:MUL(k.A,tmp.A);
}
}
sk.push_back(k);
}
int calc(){
for(int i=(int)dc.size()-1;i>=0;--i){
if(dc[i].type==3){
int nw=atoi(dc[i].token.c_str());
vector<int>tmp;
tmp.push_back(nw);
push_back((stk){1,tmp});
}else if(dc[i].type==2){
vector<int>tmp;
if(dc[i].token=="X")
tmp.push_back(0),tmp.push_back(1);
else tmp.push_back(n);
push_back((stk){1,tmp});
}else{
if(dc[i].token=="$-"){
for(int&x:sk.back().A)x=md-x;
}else if(dc[i].token=="*:"){
SQR(sk.back().A);
}else if(dc[i].token=="+/"){
FOLD(sk.back().A);
}else if(dc[i].token=="+"){
sk.push_back((stk){2,vector<int>()});
}else if(dc[i].token=="-"){
sk.push_back((stk){3,vector<int>()});
}else if(dc[i].token=="*"){
sk.push_back((stk){4,vector<int>()});
}else if(dc[i].token==")"){
sk.push_back((stk){5,vector<int>()});
}else if(dc[i].token=="("){
stk res=sk.back();
sk.pop_back();
if(sk.empty()||sk.back().tp!=5){
cerr<<"Error!"<<'\n';
exit(0);
}
sk.pop_back();
push_back(res);
}
}
}
if((int)sk.size()!=1||(int)sk[0].A.size()!=1){
cerr<<"Wrong!"<<'\n';
exit(0);
}
return sk[0].A[0];
}
int main(){
freopen("j.in","r",stdin);
freopen("j.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
for(int i=0;i<n;++i){
int x;
cin>>x;
sum[1]=(sum[1]+x)%md;
X[1].push_back(x);
X[0].push_back(1);
}
sum[0]=n;
init();
cin>>expr;
work();
cout<<calc()<<'\n';
return 0;
}
NF
题目大意:
定义 $f_{i,j}$:
现在给定 $a,b,c$ 以及 $l_{1..n}$,$t_{1..n}$,求 $f_{n,n}$ 对 $10^6+3$(是个质数)取模的结果。
题解:
被强行灌输了一些高级的数学知识,不过还是可以用简单的方法理解
首先考虑 $c=0$ 时的做法。$f_{i,j}=a\cdot f_{i,j-1}+b\cdot f_{i-1,j}$。
考虑式子的组合意义,这是一个经典的格路计数问题,其中向右走贡献乘 $a$,向下走贡献乘 $b$。则从 $(1,1)$ 到 $(m,n)$ 的贡献就是 $\binom{n+m-2}{n-1}\cdot a^{n-1}b^{m-1}$。
由于第一行第一列的初始贡献不同,因此对于每个起点都要计算。时间复杂度 $O(n)$。
现在考虑 $c\neq 0$ 的做法。我们希望找到一个办法来消掉常数项 $c$。
考虑找到一个 $x$ 满足 $x=ax+bx+c$,这样就可以得到 $f_{i,j}-x=a\cdot (f_{i,j-1}-x)+b\cdot (f_{i-1,j}-x)$。令 $g_{i,j}=f_{i,j}-x$,将 $g_{n,n}$ 用 $c=0$ 时的做法求出,再加上 $x$ 即可。
容易解得 $x=\frac{c}{1-a-b}$。
上面的做法当 $a+b\not\equiv 1\pmod{10^6+3}$ 时是正确的,否则就无法找到这样的 $x$。
虽然好像并没有这样的数据但还是要考虑的
现在的式子为 $f_{i,j}=a\cdot f_{i,j-1}+(1-a)\cdot f_{i-1,j}+c$。
我们还是想要消掉这个常数 $c$。
注意此时右边两项的系数和为 $1$,且下标和相等,因此我们考虑一个与 $(i+j)$ 有关的函数,为了方便记为 $h_{i,j}$。
令 $h_{i,j}=k(i+j)$,则 $k(i+j)=k(i+j-1)+c$。
解得 $k=c$,即 $h_{i,j}=c(i+j)$。
可以得到 $(f_{i,j}-h_{i,j})=a\cdot(f_{i,j-1}-h_{i,j-1})+(1-a)\cdot(f_{i-1,j}-h_{i-1,j})$。
令 $g_{i,j}=f_{i,j}-h_{i,j}$,将 $g_{n,n}$ 用 $c=0$ 时的做法求出,再加上 $2n\cdot c$ 就是答案。
时间复杂度 $O(n)$。
Code:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=4e5+5,md=1e6+3;
int n,R[N],C[N],a,b,c,A[N],B[N],fac[N],iv[N];
inline int pow(int a,int b){
int res=1;
for(;b;b>>=1,a=(LL)a*a%md)if(b&1)res=(LL)res*a%md;
return res;
}
inline int binom(int n,int m){return(LL)fac[n]*iv[m]%md*iv[n-m]%md;}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>a>>b>>c;
for(int i=*A=*B=*fac=1;i<=2*n;++i)A[i]=(LL)A[i-1]*a%md,B[i]=(LL)B[i-1]*b%md,fac[i]=(LL)fac[i-1]*i%md;
iv[n]=pow(fac[n],md-2);
for(int i=n-1;~i;--i)iv[i]=(i+1LL)*iv[i+1]%md;
for(int i=1;i<=n;++i)cin>>R[i];
for(int i=1;i<=n;++i)cin>>C[i];
if((a+b)%md==1){
int ans=0;
for(int i=2;i<=n;++i)
ans=(ans+((LL)A[n-1]*B[n-i]%md*(R[i]-c*(i+1LL)%md+md)+(LL)B[n-1]*A[n-i]%md*(C[i]-c*(i+1LL)%md+md))%md*binom(2*n-i-2,n-2))%md;
cout<<(ans+2LL*c*n)%md<<'\n';
}else{
int x=c*(LL)pow(2*md+1-a-b,md-2)%md,ans=0;
for(int i=2;i<=n;++i)
ans=(ans+((LL)A[n-1]*B[n-i]%md*(R[i]-x+md)+(LL)B[n-1]*A[n-i]%md*(C[i]-x+md))%md*binom(2*n-i-2,n-2))%md;
cout<<(ans+x)%md<<'\n';
}
return 0;
}
GK
题目大意:
有 $n$ 个正整数 $a_1,a_2,\ldots,a_n$,满足 $\forall k\in[2,n]$,$\sum\limits_{i=1}^{k-1}a_i \lt a_k$,且 $\sum\limits_{i=1}^n a_i\leq 2^{64}$。还有一个奇数 $r$。
现在给你 $n$ 以及 $b_1,b_2,\ldots,b_n$,其中 $b_i=a_i\cdot r\bmod{2^{64}}$。
再给你整数 $s$,要求从 $n$ 个数中选出若干个 $b_i$ 使得它们的和模 $2^{64}$ 恰好为 $s$。
保证有解。
$1\leq n\leq 64$,$1\leq b_i,r\lt 2^{64}$,$0\leq s\lt 2^{64}$。
题解:
用若干个 $b_i$ 拼出 $s$,相当于用若干个 $a_i$ 拼出 $\frac{s}r$,由题目条件可知解唯一。
我们考虑以下两个算法:
将 $n$ 个数分成 $\lfloor\frac n 2\rfloor$ 个和 $\lceil\frac n 2\rceil$ 个的两组,对每组中的每个子集计算和。再枚举其中一组的所有子集,并快速判断另一组中有无集合的和与当前的和加起来恰好为 $s$。
即 Meet in the middle。
可以使用哈希表做到 $O(2^{n/2})$ 的复杂度。
发现 $b_i$ 是与 $a_i$ 对应的,因此考虑枚举 $a_1$ 的取值,并解出 $r$,从而解出 $a’_2,a’_3,\ldots,a’_n$。
判断 $a’$ 是否满足题目中的限制条件。若满足则从大到小枚举 $a’$,并贪心地选取,即可得到方案。
考虑该算法的复杂度。由题目条件可知,$a_i>2a_{i-1}$,从而可以推出 $a_1$ 最大不超过 $2^{64-n}$。
因此复杂度为 $O(2^{64-n}\cdot n)$。
不过这里我们要考虑一些细节。
我们在求解 $r$ 的时候,是根据 $a_1\cdot r\equiv b_1\pmod{2^{64}}$。
令 $k=\texttt{__builtin_ctz}(b_1)$(即 $b_1$ 二进制末尾 $0$ 的个数)。由于 $r$ 是奇数,故 $\texttt{__builtin_ctz(a_1)}=k$ 成立。
将等式两边同时除以 $2^k$ 后得 $a_1\cdot r\cdot 2^{-k}=b_1\cdot 2^{-k}\pmod{2^{64-k}}$。
因此我们得到的 $r$ 只能保证前 $64-k$ 位是正确的。
那么我们还需要枚举后面的 $k$ 位。
看上去复杂度会变高的样子。注意到 $a_1$ 末尾要有恰好 $k$ 个 $0$,因此我们枚举的时候每次加上 $2^{k+1}$ 即可。这样算上枚举后面 $k$ 的复杂度,仍然是 $O(2^{64-n}\cdot n)$ 的。
两种算法分别在 $n$ 较小和 $n$ 较大时有着良好的表现,因此我们设一个阈值 $B$,当 $n\leq B$ 时使用算法一,当 $n>B$ 时使用算法 $2$。
$B$ 约为 $42$ 左右较优。
Code:
#include<bits/stdc++.h>
using namespace std;
#define int uint64_t
int b[64],n,s,d[64];
unordered_map<int,int>mp;
void solve1(){
int _=n/2,__=n-_;
for(int32_t i=0;i<(1<<_);++i){
int s=0;
for(int j=0;j<_;++j)if(i>>j&1)s+=b[j];
mp[s]=i;
}
for(int32_t i=0;i<(1<<__);++i){
int t=0;
for(int j=0;j<__;++j)if(i>>j&1)t+=b[_+j];
if(mp.count(s-t)){
int k=mp[s-t]|((int)i<<_);
for(int h=0;h<n;++h)cout.put((k>>h&1)^'0');
return;
}
}
}
inline int inv(int b){
int res=1,k=b;
for(int i=1;i<64;++i)
if(k>>i&1)k+=b<<i,res|=1llu<<i;
return res;
}
bool chk(){
int res=d[0];
for(int i=1;i<n;++i){
if(res>=d[i]||res>=-d[i])return 0;
res+=d[i];
}
return 1;
}
void solve2(){
int _=b[0]&-b[0],__=__builtin_ctzll(_);
for(d[0]=_;;d[0]+=_<<1){
int iv=d[0]/_*inv(b[0]/_);
for(int c=0;c<_;++c){
for(int i=1;i<n;++i)d[i]=b[i]*iv;
if(chk()){
s*=iv;
int ans=0;
for(int i=n-1;~i;--i)if(s>=d[i])ans|=1llu<<i,s-=d[i];
for(int i=0;i<n;++i)cout.put((ans>>i&1)^'0');
return;
}
iv+=1llu<<(64-__);
}
}
}
main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
for(int i=0;i<n;++i)cin>>b[i];
cin>>s;
if(n<=42)solve1();
else solve2();
return 0;
}
LK
题目大意:
有 $n$ 个旋钮,每个旋钮上有 $7$ 个数字,指针恰好指向其中一个数字。这个旋钮表示的数是从指针开始顺时针将所有数字依次排列得到的数。
你现在每次可以选择一段区间的旋钮,将它们任意旋转同一个角度(必须保证指针仍指向一个数字)。
要求使用最少的操作,使得每个旋钮表示的数都是它能表示的最大的数。求最小操作次数。
$n\leq 500$。
题解:
一个旋钮要么怎么转的大小都是一样,要么恰有一个最大数。我们可以把怎么转都一样的旋钮去掉不考虑。
以下运算默认都在模 $7$ 意义下进行。
记录 $a_i$ 表示旋钮 $i$ 顺时针旋转到最大值所需转过的数字个数。那么一次旋转相当于区间加。
记录 $b_i$ 表示 $a_i-a_{i-1}$。则一次旋转相当于选 $i,j,k$,令 $b_i$ 加上 $k$,$b_j$ 减去 $k$。
那么我们就是要将 $b$ 分成若干组,使得每组的和为 $0$。设分成了 $k$ 组,那么不难发现需要 $n-k$ 次操作。
所以要最大化 $k$。
首先去掉 $b_i=0$ 的数,然后将 $1$ 和 $6$, $2$ 和 $5$,$3$ 和 $4$ 尽可能匹配(先匹配掉一定优)。
剩下的还有最多三种数,我们可以 dp 求解。
令 $f_{i,j,k,t}$ 表示三种数分别为 $i,j,k$,最后一组模 $7$ 余 $t$ 时所需的最少操作次数。转移枚举选哪个即可。
时间复杂度 $O(n^3)$。
Code:
#include<bits/stdc++.h>
using namespace std;
const int N=505;
int n,a[N],b[N],ans,tot[8];
string s;
int A[4],B[4],m;
inline void upd(int&a,int b){a=a<b?b:a;}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;++i){
cin>>s;
string t=s;
t.erase(t.begin()),t+=s[0];
if(s==t)--n,--i;
else{
t=s,a[i]=0;
for(int j=1;j<7;++j){
s+=s[0],s.erase(s.begin());
if(s>t)t=s,a[i]=j;
}
}
b[i]=(a[i]-a[i-1]+7)%7;
}
b[n+1]=(7-a[n])%7;
if(!n)return cout<<"0\n",0;
ans=++n;
for(int i=1;i<=n;++i)++tot[b[i]];
ans-=*tot;
for(int i=1;i<4;++i){
int x=min(tot[i],tot[7-i]);
tot[i]-=x,tot[7-i]-=x,ans-=x;
}
for(int i=1;i<7;++i)if(tot[i])
A[++m]=i,B[m]=tot[i];
int dp[B[1]+2][B[2]+2][B[3]+2][7];
memset(dp,-1,(B[1]+2)*(B[2]+2)*(B[3]+2)*28);
dp[B[1]][B[2]][B[3]][0]=0;
for(int i=B[1];~i;--i)
for(int j=B[2];~j;--j)
for(int k=B[3];~k;--k)
for(int t=0;t<7;++t){
int x=dp[i][j][k][t];
if(x!=-1){
int f=(t+A[1])%7,g=(t+A[2])%7,h=(t+A[3])%7;
if(i)upd(dp[i-1][j][k][f],x+!f);
if(j)upd(dp[i][j-1][k][g],x+!g);
if(k)upd(dp[i][j][k-1][h],x+!h);
}
}
ans-=****dp;
cout<<ans<<'\n';
return 0;
}
IJ
题目大意:
这是一道 IO 交互题。
给定长度为 $n$($n$ 为偶数) 的 01 字符串 $S$。
你可以向交互库进行询问。你可以向交互库输出一个长度为 $n$ 的 01 字符串 $Q$。设 $S$ 和 $Q$ 有 $k$ 个对应的位置上的字符相同。若 $k=n$ 或 $k=\frac n 2$,则交互库将返回 $k$,否则交互库将返回 $0$。
你最多向交互库询问 $n+500$ 次,要求求出 $S$。你只需要使最后一次询问的返回值为 $n$ 即可。
题解:
考虑一个上限为 $2n$ 次询问的构造。
随便找一个 01 串 $t$,从前往后依次翻转(之前的翻转对之后生效),直到询问出一个 $\frac n 2$ 的。这里只需要不超过 $n-1$ 次询问。
假设一开始有 $k$ 个位置相等,则最后一次有 $n-k$ 个位置相等,翻转一个位置只会使 $k$ 增加或减少 $1$。而 $\frac n 2$ 在它们中间,所以一定有一个位置是 $\frac n 2$。
现在 $t$ 已经有 $\frac n 2$ 个位置正确了。
然后枚举位置 $i$,翻转 $i$ 和 $i+1$(仅这次询问翻转)并询问。若结果为 $0$,则这两个位置同时正确或错误。若结果为 $\frac n 2$,则这两个位置有一个正确,另一个错误。
有了所有相邻两个的信息,我们只需要确定一个位置就可以推出所有的位置。再花 $2$ 次询问即可。
我们来算一下恰好有 $\frac n 2$ 位正确的字符串的占比,为 $\frac{\binom{n}{n/2}}{2^n}$。当 $n=1000$ 时,用 Ubuntu 20.04 下的计算器计算出来的结果为 $0.025225018$。那我们随机 $499$ 次都随不到一个这样的串的概率为 $(1-0.025225018)^{499}\approx0.000002906$。
这个概率非常地小,所以我们直接随机得到一个恰有 $\frac n 2$ 个位置正确的串即可,并不需要那个 $n-1$ 次的构造方案了。
Code:
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int n;
bool df[N];
char s[N];
int main(){
srand(time(0)+(size_t)new int);
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1,r;;++i){
for(int j=0;j<n;++j)s[j]=(rand()&1)+'0';
cout<<s<<endl;
cin>>r;
if(r==n)return 0;
if(r==n/2)break;
}
for(int i=0,r;i+1<n;++i){
s[i]^=1,s[i+1]^=1;
cout<<s<<endl;
cin>>r;
if(r==n)return 0;
df[i]=(r==n/2)^(s[i]!=s[i+1]);
s[i]^=1,s[i+1]^=1;
}
int r;
s[0]='0';
for(int i=1;i<n;++i)s[i]=s[i-1]^df[i-1];
cout<<s<<endl;
cin>>r;
if(r==n)return 0;
for(int i=0;i<n;++i)s[i]^=1;
cout<<s<<endl;
cin>>r;
if(r!=n)return 1;
return 0;
}
IB
题目大意:
求第 $n$ 个不含前导 $0$ 的正整数,满足它的十进制表示是它的二进制表示的后缀。称这样的数为二又十进制数。
$n\leq 10^4$。
题解:
大胆猜测第 $10^4$ 个二又十进制数的位数并不会非常大(事实上最大时只有约 $200$ 位),因此可以考虑一种方式进行搜索。
一个比较方便的做法是按照数在十进制下的位数从小到大进行 BFS。
那么我们如何扩展状态呢?
假设当前十进制下有 $k$ 位,那么新加的一位是 $10^k$,而二进制上新加的一位是 $2^k$。由于 $10^k$ 必定是 $2^k$ 的倍数,因此不会导致二进制表示下的后缀产生变化。
然后我们只需要判断一下新的数模 $2^{k+1}$ 是否等于该数“对应”的二进制数即可。
当然也需要把没加 $10^k$ 的含前导 $0$ 的数放入队列,用于在之后的位上添加 $1$。
由于在搜索同一个位数的时候没有安装数的大小顺序,因此需要搜出较多个数以后,再排序输出第 $n$ 个。
由于可能涉及到的高精度运算,代码使用 Java 实现。
Code:
import java.util.*;
import java.math.*;
import java.io.*;
public class Main{
static int n;
static BigInteger _2[]=new BigInteger[205],_10[]=new BigInteger[205];
public static class data{
BigInteger decimal,binary;
int w;
boolean zero;
data(){}
data(BigInteger dec,BigInteger bin,int ww,boolean zr){
decimal=dec;
binary=bin;
w=ww;
zero=zr;
}
}
static data q[]=new data[100005];
static ArrayList res=new ArrayList();
public static void main(String args[]){
try{
System.setIn(new FileInputStream("binary.in"));
}catch(FileNotFoundException fnfe){
System.out.println(fnfe.getMessage());
}
try{
System.setOut(new PrintStream("binary.out"));
}catch(FileNotFoundException fnfe){
System.out.println(fnfe.getMessage());
}
Scanner in=new Scanner(System.in);
n=in.nextInt();
_2[0]=_10[0]=BigInteger.valueOf(1);
for(int i=1;i<=200;++i){
_2[i]=_2[i-1].multiply(BigInteger.valueOf(2));
_10[i]=_10[i-1].multiply(BigInteger.valueOf(10));
}
int h=1,t=0;
q[++t]=new data(BigInteger.valueOf(0),BigInteger.valueOf(0),0,false);
q[++t]=new data(BigInteger.valueOf(1),BigInteger.valueOf(1),0,true);
int cnt=0;
while(h<=t){
data x=q[h++];
if(x.zero)res.add(cnt++,x.decimal);
if(cnt==16384)break;
++x.w;
x.zero=false;
if(x.decimal.remainder(_2[x.w+1]).compareTo(x.binary)==0)
q[++t]=new data(x.decimal,x.binary,x.w,x.zero);
x.decimal=x.decimal.add(_10[x.w]);
x.binary=x.binary.add(_2[x.w]);
x.zero=true;
if(x.decimal.remainder(_2[x.w+1]).compareTo(x.binary)==0)
q[++t]=new data(x.decimal,x.binary,x.w,x.zero);;
}
Collections.sort(res);
System.out.println((BigInteger)res.get(n-1));
}
}
TK
题目大意:
你有 $n$ 个烤肉串要依次烤。你在做烤肉串的时候可能会做白日梦,任意连续 $t+1$ 秒内你只能有 $1$ 秒做白日梦。
第 $i$ 个烤肉串要加 $q_i$ 单位原料,加入 $1$ 单位原料要花 $1$ 秒。做白日梦时会少加入 $1$ 单位原料。客人对第 $i$ 个烤肉串的最少原料需求是 $x_i$,也就是说做第 $i$ 个烤肉串的时候最多能做 $q_i-t_i$ 秒的白日梦。
求有多少种不同的做白日梦的方案,使得客人对所有烤肉串满意。
$1\leq n\leq 1000$,$0\leq t\leq 100$,$1\le q_i\leq 250$,$0\leq x_i\leq q_i$。
题解:
总时长为 $\sum_i q_i\leq 250000$,考虑直接对每个时刻进行 dp。
令 $dp_{i,j}$ 表示第 $i$ 个时刻结束后,当前烤肉串已经做了 $j$ 秒白日梦时的方案数。
转移有两种:不做白日梦和做白日梦,分别从第 $i-1$ 秒和第 $i-t-1$ 秒转移过来。
如果被转移的状态的烤肉串和当前烤肉串不同,则 $j$ 需重新计,否则 $j$ 不能超过这个烤肉串的上限。
时空复杂度 $O(nq^2)$。常数较小,在时空上都没有压力。
Code:
#include<bits/stdc++.h>
using namespace std;
const int N=250005,md=1e9+7;
typedef long long LL;
int n,t,bel[N],A[1234],B[1234],m;
int dp[N][251],sum[N];
int main(){
freopen("kebab.in","r",stdin);
freopen("kebab.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>t;
for(int i=1;i<=n;++i){
cin>>A[i]>>B[i];
for(int j=1;j<=A[i];++j)
bel[m+j]=i;
m+=A[i];
}
sum[0]=dp[0][0]=1;
for(int i=1;i<=m;++i){
int x=bel[i],lm=A[x]-B[x];
dp[i][0]=dp[i-1][0];
if(bel[i-1]!=bel[i])
dp[i][0]=sum[i-1];
int pv=max(0,i-t-1);
if(bel[pv]!=x&&lm)dp[i][1]=((bel[i-1]==x)*dp[i-1][1]+sum[pv])%md;
else{
for(int j=1;j<=lm;++j)
dp[i][j]=((bel[i-1]==x)*dp[i-1][j]+dp[pv][j-1])%md;
}
for(int j=0;j<=lm;++j)sum[i]=(dp[i][j]+sum[i])%md;
}
cout<<sum[m]<<'\n';
return 0;
}
PD
题目大意:
有 $n$ 个站点和 $m$ 条线路。每条线路经过若干个站点(不重复),且都是双向的。
坐在一条线路上从一个站点到另一个站点需要 $1$ 分钟。换乘不需要时间(从一条线路到它的相反方向也要换乘)。
现在需要从 $s$ 走到 $t$,求最少的换乘次数和在此基础上花费的最多时间。
$n\leq 3\times 10^5$,$m\leq 10^5$,线路总长 $\leq 10^6$。
输入格式比较烦。
题解:
主要是对输入的处理。
由于站点名中没有空格,因此使用 cin 直接读入还是比较方便的。以读一条线路为例,先把开头读掉,然后一直读直到末尾不是逗号为止。
对于最少换乘次数,直接建图跑最短路即可。由于只有 01 边权所以可以直接使用队列(我还是使用了优先队列)。
然后我们按照换乘次数对图进行分层,只保留相邻两层和同层中的有向边。
由于只有在换乘的时候跨层,而同层中的边都是线路上的有向边,因此不难发现是个有向无环图。
使用 BFS 按照拓扑排序的方式求最长路即可。
Code:
#include<bits/stdc++.h>
using namespace std;
const int N=2e6+5;
typedef uint64_t LL;
map<string,int>mp;
int T;
string s,station[N];
int n,k,c,head[N],cnt,st,ed;
pair<int,int>dis[N];
inline pair<int,int>operator+(const pair<int,int>&a,const pair<int,int>&b){
return make_pair(a.first+b.first,a.second+b.second);
}
struct edge{
int to,nxt;pair<int,int>w;
}e[N*3];
inline void addedge(int u,int v,pair<int,int>w){e[++cnt]=(edge){v,head[u],w},head[u]=cnt;}
struct data{
int u;pair<int,int>d;
inline bool operator<(const data&rhs)const{return d>rhs.d;}
};
priority_queue<data>q;
void Kosaraju(){
for(int i=1;i<=k;++i)dis[i]=make_pair(0x3f3f3f3f,0x3f3f3f3f);
dis[st]=make_pair(0,0);
q.push((data){st,dis[st]});
while(q.size()){
data w=q.top();q.pop();
int u=w.u;
if(dis[u]!=w.d)continue;
for(int i=head[u];i;i=e[i].nxt)
if(dis[e[i].to]>dis[u]+e[i].w){
dis[e[i].to]=dis[u]+e[i].w;
q.push((data){e[i].to,dis[e[i].to]});
}
}
}
queue<int>p;
bool vis[N];
int deg[N];
void Johnson(){
for(int x=1;x<=k;++x)
for(int i=head[x];i;i=e[i].nxt)if(dis[e[i].to].first==dis[x].first+e[i].w.first)
++deg[e[i].to];
for(int i=1;i<=k;++i)if(!deg[i])p.push(i);
while(p.size()){
int u=p.front();p.pop();
for(int i=head[u];i;i=e[i].nxt)
if(dis[e[i].to].first==dis[u].first+e[i].w.first){
dis[e[i].to].second=max(dis[e[i].to].second,dis[u].second+e[i].w.second);
if(!--deg[e[i].to])p.push(e[i].to);
}
}
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
for(cin>>T;T--;){
memset(head,0,sizeof head),cnt=0;
mp.clear();
n=c=0;
cin>>s;
for(;;){
bool ok=1;
cin>>s;
if(s.back()==',')
ok=0,s.pop_back();
station[++n]=s;
mp[s]=n;
if(ok)break;
}
k=n;
cin>>s;
for(;;){
bool ok=1;
cin>>s;
if(s.back()==',')
ok=0,s.pop_back();
++c;
if(ok)break;
}
while(c--){
cin>>s>>s;
static int id[N],_[N];
int tot=0;
for(;;){
bool ok=1;
cin>>s;
if(s.back()==',')
ok=0,s.pop_back();
id[++tot]=mp[s];
if(ok)break;
}
for(int i=1;i<=tot;++i){
_[i]=++k;
addedge(id[i],_[i],make_pair(1,0));
addedge(_[i],id[i],make_pair(0,0));
}
for(int i=1;i<tot;++i)
addedge(_[i],_[i+1],make_pair(0,1));
for(int i=1;i<=tot;++i){
_[i]=++k;
addedge(id[i],_[i],make_pair(1,0));
addedge(_[i],id[i],make_pair(0,0));
}
for(int i=tot;i>1;--i)
addedge(_[i],_[i-1],make_pair(0,1));
}
cin>>s>>s>>s>>s;
st=mp[s];
cin>>s>>s>>s>>s;
ed=mp[s];
Kosaraju();
Johnson();
int A=dis[ed].second,B=dis[ed].first;
cout<<"optimal travel from "+station[st]+" to "+station[ed]+": "
<<B<<(B==1?" line, ":" lines, ")<<A<<(A==1?" minute\n":" minutes\n");
}
return 0;
}
QG
题目大意:
给定一张 $n$ 个点 $m$ 条边的简单无向图,要求找到两个不同的点 $s,t$,满足它们之间有三条不经过重复边、除了起点和终点不经过重复点的路径。
如果有则输出一种方案,没有则输出 -1。
$n,m\leq 10^5$。
题解:
见CF521E。
Code:
#include<cstdio>
#include<cstdlib>
#include<vector>
const int N=2e5+6;
struct edge{
int to,nxt;
bool vis;
}e[N<<1];
int head[N],cnt,n,m,dep[N],fa[N],up[N];
bool vis[N],isret;
std::vector<int>out;
void O_R(int now,const int&ed){
if(now!=ed)O_R(fa[now],ed);
out.push_back(now);
}
void output(){
printf("%d",(int)out.size());
for(int i=0;i<(int)out.size();++i)printf(" %d",out[i]);
putchar('\n');
out.clear();
}
void DFS(int now,int pre){
if(isret)return;
vis[now]=1;
for(int i=head[now];i;i=e[i].nxt)
if(i!=pre&&!vis[e[i].to]){
e[i].vis=1;
dep[e[i].to]=dep[now]+1;
fa[e[i].to]=now;
DFS(e[i].to,i^1);
if(isret)return;
}else
if(dep[e[i].to]<dep[now]&&i!=pre){
if(!up[now])up[now]=e[i].to;
else{
int u=up[now],v=e[i].to;
if(dep[u]<dep[v])u^=v^=u^=v;
out.push_back(now);
for(int s=now;s!=u;s=fa[s])out.push_back(fa[s]);
printf("%d %d\n",out[0],out.back());
output();
printf("2 %d %d\n",now,u);
out.push_back(now);
O_R(u,v);
output();
isret=1;return;
}
}
}
int dfs(int now){
if(isret)return 0;
int res=up[now]?now:0;
for(int i=head[now];i;i=e[i].nxt)
if(e[i].vis){
int t=dfs(e[i].to);
if(isret)return 0;
if(up[t]==now)t=0;
if(res&&t){
int u=up[res],v=up[t];
if(dep[u]<dep[v])u^=v^=u^=v,res^=t^=res^=t;
O_R(res,now),out.push_back(u);
printf("%d %d\n",out[0],out.back());
output();
out.push_back(now);
for(int s=now;s!=u;s=fa[s])out.push_back(fa[s]);
output();
O_R(t,now),O_R(u,v);
output();
isret=1;return 0;
}else if(t)res=t;
}
return res;
}
int main(){
int T;
freopen("grand.in","r",stdin);
freopen("grand.out","w",stdout);
for(scanf("%d",&T);T--;){
isret=0;
for(int i=1;i<=n;++i)head[i]=fa[i]=up[i]=dep[i]=0,vis[i]=0;
cnt=1;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i){
int u,v;
scanf("%d%d",&u,&v);
e[++cnt]=(edge){v,head[u]},head[u]=cnt;
e[++cnt]=(edge){u,head[v]},head[v]=cnt;
}
for(int i=1;i<=n;++i)if(!dep[i])dep[i]=1,DFS(i,0);
for(int i=1;i<=n;++i)if(dep[i]==1)dfs(i);
if(!isret)puts("-1");
}
return 0;
}
QC
题目大意:
给定一个由小写字母组成的字符串 $S$。定义 a,e,i,o,u,y,w 为元音字母,其他为辅音字母。
要求改变其中一些字符的大小写,使得:
- 同种字母小写一致。
- 令满足一个大写,另一个小写的相邻的辅音字母对有 $c$ 对,这个 $c$ 最大。
输出最大的 $c$。
$|S|\leq 10^6$。
题解:
辅音字母一共有 $26-7=19$ 个,由于每个字母大小写必须一样,所以辅音字母的不同情况有 $2^{19}$ 种。我们并不需要关系元音字母的大小写。
令 $f(c_1,c_2)$ 表示 $c_1$ 和 $c_2$ 相邻出现的次数。枚举辅音字母的大小写情况,然后 $O(19^2)$ 计算这个情况的符合条件的字母对个数即可。足以通过本题。
Code:
#include<bits/stdc++.h>
using namespace std;
int id[200],cnt[23][23];
char s[1000005];
int main(){
freopen("consonant.in","r",stdin);
freopen("consonant.out","w",stdout);
memset(id,-1,sizeof id);
int $=0;
for(int i='b';i<='z';++i)
if(i!='e'&&i!='i'&&i!='o'&&i!='u'&&i!='y'&&i!='w')id[i]=$++;
cin>>s;
for(int i=0;s[i+1];++i){
int x=id[s[i]],y=id[s[i+1]];
if(x>y)swap(x,y);
if(x!=-1&&y!=-1)++cnt[x][y];
}
int res=0,mx=0;
for(int S=0;S<1<<$;++S){
int nw=0;
for(int i=0;i<$;++i)
for(int j=i+1;j<$;++j)if((S>>i&1)^(S>>j&1))nw+=cnt[i][j];
if(mx<nw)mx=nw,res=S;
}
for(int i=0;s[i];++i)if(id[s[i]]!=-1&&(res>>id[s[i]]&1))s[i]=toupper(s[i]);
cout<<s<<'\n';
return 0;
}
UC
题目大意:
给定字符串 $S,T$,你需要执行一个命令 s/<string>/<replacement>/g,该操作的作用如下(为了方便描述,令字符串 $A,B$ 分别表示 <string> 以及 <replacement>):
在 $S$ 中找到第一次出现
<string>的位置,令 $S=S_L+A+S_R$。如果找不到 $A$,则 $S$ 就是结果。
- 设 $R$ 为对 $S_R$ 执行
s/A/B/g命令的结果。 - 则最终的结果就是 $S_L+B+R$。
现在要求你找到这样一条命令并对 $S$ 执行,使得执行完毕后 $S$ 与 $T$ 完全相等。
其中 <string> 不得是空串,<replacement> 可以为空。
$|S|,|T|\leq 2000$。
题解:
考虑使用字符串 hash 解决这个问题。
我们对 $S$ 和 $T$ 的每个子串求出 hash 值,对每个不同的 hash 值,从小到大储存它的出现位置。
然后枚举 $S$ 和 $T$ 的每个 hash 值,以及它们的出现位置,把重合的位置删掉,并计算出将当前考虑的 hash 值代表的串删去后这个串的 hash 值,分别存入 $v_S$ 和 $v_T$。为了避免一些情况产生的冲突,需要在删除的位置加上特殊字符替代。
然后在 $v_S$ 和 $v_T$ 中找到两个一样的 hash 值,就代表存在替换的方法,输出即可。如果找不到,则说明无解。
$S$ 和 $T$ 的子串个数只有 $O(n^2)$ 个,因此可以得到时间复杂度。
时间复杂度 $O(n^2)$(使用哈希表存储不同的 hash 值)或 $O(n^2\log n)$(对 hash 值离散化),由于常数较大,并不足以通过本题。
事实上,对于 $S$ 中的每个不同的 $A$,我们都能唯一确定 $B$ 的长度及其应该在的位置,原因如下:
- 假设替换了 $k$ 个 $A$ 变成 $k$ 个 $B$,则有 $|S|-k|A|+k|B|=|T|$,即 $|S|-|T|=k(|A|+|B|)$。
则我们只需要处理 $S$ 的子串的 hash 值并枚举它,并记录每个需要替换成 $B$ 串的位置,以及计算出 $B$ 串的长度。于是我们只需要判断这些位置在 $T$ 中表示的串是否相同即可。
时间复杂度不变,但常数上有显著优化。使用单模式的 hash,再加上其他地方的实现稍微好一点,即可通过本题。
Code:
#include<bits/stdc++.h>
using namespace std;
const int N=2048,md1=1004535809;
typedef uint64_t LL;
mt19937 mt(time(0)+(size_t)new int);
vector<int>va;
char s[N],t[N];
int lens,lent,_1[N],head[4050002],cnt,to[4050002],nxt[4050002],_len[4050002];
int base1;
int L1,R1,L2,R2,lenans=114514;
int HA1[N],HB1[N];
vector<int>_L;
inline int get_ha1(int l,int r){
if(l>r)return 0;
return(HA1[r]+md1-(LL)HA1[l-1]*_1[r-l+1]%md1)%md1;
}
inline int get_hb1(int l,int r){
if(l>r)return 0;
return(HB1[r]+md1-(LL)HB1[l-1]*_1[r-l+1]%md1)%md1;
}
void init(){
for(int i=1;i<=lens;++i){
HA1[i]=((LL)HA1[i-1]*base1+s[i])%md1;
}
for(int i=1;i<=lent;++i){
HB1[i]=((LL)HB1[i-1]*base1+t[i])%md1;
}
}
inline void add(int x,int v){++cnt,to[cnt]=v,nxt[cnt]=head[x],head[x]=cnt;}
int main(){
freopen("curiosity.in","r",stdin);
freopen("curiosity.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin.getline(s+1,12243),cin.getline(t+1,12243);
lens=strlen(s+1),lent=strlen(t+1);
base1=mt()%1000+500;
for(int i=*_1=1;i<=2000;++i)
_1[i]=(LL)_1[i-1]*base1%md1;
init();
for(int i=lens;i;--i){
int hx1=0;
for(int len=1;i+len-1<=lens;++len){
hx1=((LL)hx1*base1+s[i+len-1])%md1;
va.push_back(hx1);
}
}
sort(va.begin(),va.end());va.erase(unique(va.begin(),va.end()),va.end());
for(int i=lens;i;--i){
int hx1=0;
for(int len=1;i+len-1<=lens;++len){
hx1=((LL)hx1*base1+s[i+len-1])%md1;
int id=lower_bound(va.begin(),va.end(),hx1)-va.begin();
_len[id]=len;
add(id,i);
}
}
for(int id=0;id<(int)va.size();++id){
int L=_len[id];
if(L>=lenans)continue;
int hx1=0,nw=1,ds=0;
_L.clear();
for(int i=head[id];i;i=nxt[i]){
int x=to[i];
if(x<nw)continue;
++ds;
int len=x-nw;
_L.push_back(len);
hx1=((LL)hx1*_1[len]+get_ha1(nw,x-1))%md1;
nw=x+L;
}
int _x=lens+1,_len=_x-nw;
hx1=((LL)hx1*_1[_len]+get_ha1(nw,_x-1))%md1;
if((lent-lens)%ds)continue;
int l=(lent-(lens-ds*L))/ds;
if(l<0)continue;
if(L+l>=lenans)continue;
nw=1;
int hb1=0,hs1=get_hb1(_L[0]+1,_L[0]+l);
bool ok=1;
for(int ln:_L){
hb1=((LL)hb1*_1[ln]+get_hb1(nw,nw+ln-1))%md1;
nw+=ln;
if(hs1!=get_hb1(nw,nw+l-1)){ok=0;break;}
nw+=l;
}
hb1=((LL)hb1*_1[_len]+get_hb1(nw,nw+_len-1))%md1;
ok&=hx1==hb1;
if(!ok)continue;
lenans=L+l,L1=to[head[id]],R1=L1+L-1,L2=_L[0]+1,R2=L2+l-1;
}
cout<<"s/";
for(int i=L1;i<=R1;++i)cout.put(s[i]);
cout.put('/');
for(int i=L2;i<=R2;++i)cout.put(t[i]);
cout<<"/g\n";
return 0;
}
QJ
题目大意:
给定一个不包含 $0$ 的长度为 $n$ 的序列 $a_1,a_2,\ldots,a_n$。令正数的和为 $P$,负数的和为 $N$。
如果 $a_i\gt 0$,则 $w_i=\frac{a_i}P$,否则 $w_i=\frac{a_i}{|N|}$。
令 $s_i$ 表示 $w_i$ 的前缀和,要求找到一个 $k$ 使得 $s_k$ 最大,在此基础上 $k$ 最小。你需要回答这个 $k$。
有 $m$ 次单点修改,你需要在开始和每次修改后回答这个问题。
$n,m\leq 5\times 10^4$,$a_i$ 修改前后均满足 $|a_i|\leq 10^9$ 且 $a_i\neq 0$。
题解:
令 $A_i=\sum\limits_{j=1}^i [a_j>0]a_j$,$B_i=\sum\limits_{j=1}^i [a_j<0]a_j$。
则 $A_{i}\cdot |N|+B_{i}\cdot P=P\cdot |N|\cdot s_i$。我们只需要求 $A_{i}\cdot |N|+B_{i}\cdot P$ 的最大值的位置即可。
我们假设知道了 $P$ 和 $|N|$ 的值,需要求 $A_{i}\cdot |N|+B_{i}\cdot P$ 的最大值的位置。
相当于求 $A_{i}\cdot \frac{|N|}P+B_{i}$ 的最大值的位置,这是一个非常经典的凸包问题,将 $(A_i,B_i)$ 插入凸包中然后在凸包上二分即可得到最大值及其位置。本题中 $A_i$ 单调因此可以直接插入。
对一个 $a_i$ 的修改,相当于对 $A_i$ 或 $B_i$ 的区间加操作。考虑使用分块解决。
对于整块的修改,直接打整体修改标记。对于边角修改,直接暴力修改,然后重构凸包即可。
取块大小为 $\sqrt{n\log n}$ 可以得到 $O(m\sqrt{n\log n})$ 的时间复杂度。
Code:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef __int128 LLL;
#define bel(x)((x-1)/siz+1)
const int N=50005,siz=505,K=siz+2;
int n,m,blocks,a[N],L[N],R[N];
LL sumA,sumB;
struct blo{
LL A[K],B[K],dA,dB;
int len,top;
struct point{
LL x,y;int id;
inline point operator-(const point&rhs)const{return(point){x-rhs.x,y-rhs.y,0};}
}V[K];
inline bool cross(const point&a,const point&b)const{
return(LLL)a.x*b.y>=(LLL)a.y*b.x;
}
void rebuild(){
top=0;
for(int i=1;i<=len;++i){
point x=(point){A[i],-B[i],i};
while(top>1&&cross(V[top]-V[top-1],x-V[top-1]))--top;
V[++top]=x;
}
}
inline void init(int*a,int _l,LL sA,LL sB){
len=_l;
A[0]=sA,B[0]=sB;
for(int i=1;i<=len;++i){
A[i]=A[i-1],B[i]=B[i-1];
if(a[i]>0)A[i]+=a[i];else B[i]-=a[i];
}
rebuild();
}
void modifyA(int pos,int dlt){
for(int i=pos;i<=len;++i)A[i]+=dlt;
rebuild();
}
void modifyB(int pos,int dlt){
for(int i=pos;i<=len;++i)B[i]+=dlt;
rebuild();
}
inline void find(int&p,LLL&MX,int id){
int l=2,r=top,res=1;
while(l<=r){
const int k=(l+r)/2;
LLL L=(LLL)(V[k-1].x+dA)*sumB+(LLL)(V[k-1].y-dB)*sumA;
LLL R=(LLL)(V[k].x+dA)*sumB+(LLL)(V[k].y-dB)*sumA;
if(L>=R)r=res=k-1;else l=(res=k)+1;
}
LLL X=(LLL)(V[res].x+dA)*sumB+(LLL)(V[res].y-dB)*sumA;
if(X>MX)MX=X,p=V[res].id+R[id-1];
}
}G[205];
void modifyA(int p,int dlt){
int bl=bel(p);
G[bl].modifyA(p-L[bl]+1,dlt);
for(int i=bl+1;i<=blocks;++i)G[i].dA+=dlt;
}
void modifyB(int p,int dlt){
int bl=bel(p);
G[bl].modifyB(p-L[bl]+1,dlt);
for(int i=bl+1;i<=blocks;++i)G[i].dB+=dlt;
}
void getans(){
int pos=0;LLL V=-((LLL)1<<120);
for(int i=1;i<=blocks;++i)G[i].find(pos,V,i);
cout<<pos<<'\n';
}
int main(){
freopen("joker.in","r",stdin);
freopen("joker.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;++i){
cin>>a[i];if(a[i]>0)sumA+=a[i];else sumB-=a[i];
}
blocks=bel(n);
for(int i=1;i<=blocks;++i)L[i]=R[i-1]+1,R[i]=i*siz;
R[blocks]=n;
LL sA=0,sB=0;
for(int i=1;i<=blocks;++i){
G[i].init(a+L[i]-1,R[i]-L[i]+1,sA,sB);
sA=G[i].A[siz],sB=G[i].B[siz];
}
getans();
while(m--){
int x,v;
cin>>x>>v;
if(a[x]>0)modifyA(x,-a[x]),sumA-=a[x];else modifyB(x,a[x]),sumB+=a[x];
a[x]=v;
if(a[x]>0)modifyA(x,a[x]),sumA+=a[x];else modifyB(x,-a[x]),sumB-=a[x];
getans();
}
return 0;
}
RH
题目大意:
多组询问。每次给定 $n,m$,要求用最少的正方形恰好覆盖 $n\times m$ 的矩形。输出方案。
$1\le n,m\le 60$。
题解:
本题似乎并没有较好的解决办法,因此考虑使用搜索。但由于不同的情况只有 $3600$ 种,因此可以将所有情况搜出来然后打表。
直接搜索状态数过于庞大,需要一些剪枝。
首先 $n,m$ 和 $m,n$ 的情况是对称的,只需要搜一种即可。设 $n>m$。
我们考虑每次搜索的时候,当前的状态都是下图所示的单调的折线。
+-------------------+----+
| | |
| +-------+ |
| | |
| | |
| +----+ |
| +---+ |
| | |
+--+---------------------+
然后搜索的时候枚举凹处的拐点和正方形的边长即可,注意放完后仍要保持一条单调的折线。
我们需要说明这么做的正确性。若在一个拐点处放的正方形使得折线不满足条件,则可以在它多出来的一侧继续放正方形来修正折线。而最终修正后的状态去掉一开始放的正方形,折线仍是满足条件的。
最终状态显然是满足条件的,说明无论怎么放,我们总能找到一种顺序使得它任意时刻都满足条件。故只需要这么搜索即可。
还有一个简单的剪枝是,若当前凹处拐点有 $k$ 个,则至少还要放 $k$ 个正方形才能恰好覆盖。用这个可以快速判断当前状态是否可能更新最优解,若不可能则直接退出。
如此一来,效率有了很大的提升。可是在 $n,m$ 较大的时候仍然会卡住。
尝试运行一下搜索的程序,能够发现,在正确放置前面 $1~2$ 个正方形时,程序能在较短的时间内搜出最优解,而在其他状态时往往要搜很久。因此我们可以使用卡时的方法,限制每个状态运行的最大时间。不过该方法需要仔细调整参数,否则可能搜不到最优解。根据测试,搜索前两个正方形,接下来的搜索使用卡时来优化,就能够跑出所有最优解。
然后再找一下最优解的规律,发现大部分情况都包含边长为 $m$ 或 $\frac m 2$ 的正方形,且放在边界。因此第一层搜索的时候,我们优先搜索这两个边长,即可加快搜到最优解的速度。
据此写出的代码在我的电脑上运行了 $7$ 个多小时。可以开两个进程,从两个方向分别搜,这样运行时间就可以接受了。可以通过合理调参来减少运行时间(我搜索技术不太行只能写出这种低效的东西了)。
下面是搜索代码(该代码搜出的方案和我最终提交的代码的方案并不完全一致,经过检验,对于不同的 $n,m$,它搜出的均为最优解)。
#include<bits/stdc++.h>
using namespace std;
typedef vector<pair<int,int> >vii;
#define fi first
#define se second
struct dat{
int x,y,L;
};
vector<dat>ans,A;
vii vec;
#define Main {\
vii nw=vec;\
int X=vec[i].fi-j,Y=vec[i].se-j;\
if((i&&X<vec[i-1].fi))continue;\
if((i+1<(int)vec.size()&&Y<vec[i+1].se))continue;\
if(Y&&(i+1==(int)vec.size()||Y>vec[i+1].se))nw.insert(nw.begin()+i+1,make_pair(vec[i].fi,Y));\
if(X&&(!i||X>vec[i-1].fi))nw.insert(nw.begin()+i+1,make_pair(X,vec[i].se));\
nw.erase(nw.begin()+i);\
A.emplace_back((dat){X,Y,j});\
dfs(w,h,nw);\
A.pop_back();\
if(A.size()<2)cl=clock();\
if((clock()-cl)*1./CLOCKS_PER_SEC>3)return;\
}
mt19937 mt(time(0));
clock_t cl;
void dfs(const int&w,const int&h,vii vec){
if((clock()-cl)*1./CLOCKS_PER_SEC>3)return;
if(ans.size()&&int(vec.size()+A.size())>=int(ans.size()))return;
if(vec.empty()){
if(ans.empty()||A.size()<ans.size())ans=A;
return;
}
// for(int i=(int)vec.size()-1;~i;--i){
for(int i=0;i<(int)vec.size();++i){
int m=min(vec[i].fi,vec[i].se);
if(A.size()<1){
cl=clock();
int j=m;Main
j/=2;Main
for(j=m/2+1;j<m;++j)Main
}else{
for(int j=m;j;--j)Main
}
}
}
int main(){
freopen("tbk.txt","w",stdout);
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
for(int W=1;W<=60;++W)
for(int H=1;H<W;++H){
cl=clock();
ans.clear(),A.clear();
vec.clear();
vec.emplace_back(W,H);
dfs(W,H,vec);
if(ans.empty())cerr<<"ERROR : ";
cout<<'{'<<ans.size();
for(dat i:ans)cout<<','<<i.x<<','<<i.y<<','<<i.L;
cout<<"},\n";
cout.flush();
cerr<<W<<' '<<H<<endl;
}
cout<<fixed<<setprecision(9)<<1.*clock()/CLOCKS_PER_SEC<<'\n';
return 0;
}
该程序打出来的表的大小达到了 $120\texttt{KB}$,考虑到多数评测平台以及比赛的代码长度限制都至少为 $50\texttt{KB}$,故我以此为上限,对表进行了压缩。
对于本题,由于表中的每个元素均在 $0\sim 60$ 之间,使用 char 即可存储,因此我们可以直接将一个整数映射成一个字符,然后将一组 $n,m$ 对应的状态压缩成一个字符串。
压缩后表的大小仍略多于 $50\texttt{KB}$。
我们发现,$m=1$ 和 $m=2$ 时所需要的正方形数较多,而这两种情况可以直接特判处理。因此我们把这两类情况从表中删掉,然后加上特判即可。
处理完后表长约为 $48\texttt{KB}$,足够编写剩下的代码。
Code:
#include<bits/stdc++.h>
using namespace std;
const char A[1805][400]={
"",
"","","","","'$#&#%$#$$##$","","","'%#&#$%$#$##$","($#'#&$#%$#$$##$","","","%&#&##&","&%#'#%%##%","(&%&'#%#%&%#%##%","","","('#&$#&#%$#$$##$","(&#'#$&%#$$#$##$","(%#(#&%#$%$#$##$","('&&'#&#%'%#%##%","","","((#&%#&#$%$#$##$","%'#'##'","(&#(#%&$#%#$$##$","'%#)#'%#%%##%","*'&'(#&'%$#&'&%$&#%##&","","","&)#&&#&##&",
")(#'$#'#&$#%$#$$##$",")'#(#$'&#$%#$$#$##$","&&#)#&&##&",")%#*#(%#&%#$%$#$##$","*(''(#'#&(%#&#$%$#$##$","","",")*#&'#&$#&#%$#$$##$","')#'%#'#%%##%","%(#(##(","''#)#%'%#%##%",")&#*#'&#$&%#$$#$##$","(%#+#)%#'%#%%##%",")('()#'#'(%#'#%%##%","","",")+#&(#&%#&#$%$#$##$",")*#'&#'#$&%#$$#$##$","))#('&%%&%&#&#&%##&",")(#)&'%&%%&#%#&&##&",")'#*#&'$#&#%$#$$##$",")&#+#(&#%&$#%#$$##$","*%#,#*%#(%#&%#$%$#$##$","))(()#(#')%#'#%%##%","","","',#&)#&&#&##&","&+#''#'##'",")*#(%#(#&%#$%$#$##$","%)#)##)",
")(#*#%(&#%$#%#$$##$","&'#+#''##'","'&#,#)&#&&##&","()')+#'#')'#'##'","*'&+,#&)#&#*'#&'&#&##&","","","*-#&*#&'#&$#&#%$#$$##$","*,#'(#'$#'#&$#%$#$$##$",")+#(&#(#%&$#%#$$##$",")*#)'&&'#&#%'%#%##%","))#*&'&'%%'#%#'&##'",")(#+#&(%#&#$%$#$##$","*'#,#('#$'&#$%#$$#$##$","*&#-#*&#'&#$&%#$$#$##$",")*()+#(*'$#'*'#'##'","*'&,-#&*#&'#&#+'#''##'","","","*.#&+#&(#&%#&#$%$#$##$","(-#')#'%#'#%%##%","*,#('#(#$'&#$%#$$#$##$","(+#)%#)#'%#%%##%","%*#*##*","()#+#%)'#%%#%##%","*(#,#'($#'#&$#%$#$$##$","('#-#)'#%'%#%##%","*&#.#+&#(&#%&$#%#$$##$","(+))+#)#'+'#'##'","**)*+#)#)*%#)#'%#%%##%",
"","","(/#&,#&)#&&#&##&","*.#'*#'&#'#$&%#$$#$##$","&-#((#(##(","',#)&#)#&&##&","++#*('&%'&'#'#(%$'$#'$##'","+*#+'(&'%&(#%'$$'#$#''##'","')#,#&)&#&##&","&(#-#((##(","*'#.#*'#&'$#&#%$#$$##$","(&#/#,&#)&#&&##&","+(&-/#&,#&)#&#+(#&(&#&##&","*+**+#*#)+%#)#'%#%%##%","","","+0#&-#&*#&'#&$#&#%$#$$##$","'/#'+#''#'##'","*.#()#(&%&'#%#%&%#%##%","(-#)'#)#%'%#%##%","*,#*%#*#(%#&%#$%$#$##$","%+#+##+","**#,#%*(#%&#%$#%#$$##$","()#-#')%#'#%%##%","*(#.#)(%&&%#&#'%#%%##%","''#/#+'#''##'","+�#-&#*&#'&#$&%#$$#$##$","*+)+-#)+'%#)+)'%)#'##)","*)(-.#()#(#,)#&)&#&##&","",
"","+1#&.#&+#&(#&%#&#$%$#$##$","+0#',#'(#'$#'#&$#%$#$$##$","*/#(*#(%#(#&%#$%$#$##$","*.#)(#)%&&%#&#'%#%%##%","*-#*&#*#'&#$&%#$$#$##$","+,#+(''(#'#&(%#&#$%$#$##$","++#,'('(%&)#%($$(#$#('##(","**#-#&*'#&$#&#%$#$$##$","*)#.#()&%&'#%#%&%#%##%","*(#/#*(#%(&#%$#%#$$##$","+'#0#,'#('#$'&#$%#$$#$##$","*-**-#*#'-)#'%#'#%%##%","+,*+-#*,)$#),'#)#%'%#%##%","+*)-.#)#,*')&(#)'($#('##(","","",")2#&/#&,#&)#&&#&##&",")1#'-#')#'%#'#%%##%","*0#(+#(&#(#%&$#%#$$##$","&/#))#)##)","*.#*'#*#&'$#&#%$#$$##$",")-#+%#+#)%#'%#%%##%","%,#,##,",")+#-#%+)#%'#%%#%##%","**#.#'*&#'#$&%#$$#$##$","&)#/#))##)","*(#0#+(#&(%#&#$%$#$##$",")'#1#-'#)'#%'%#%##%","(,),/#)#),)#)##)",
"*-++-#+#)-'#)#%'%#%##%","+,+,-#+#+,%#+#)%#'%#%%##%","","",",3#&0#&-#&*#&'#&$#&#%$#$$##$","+2#'.#'*#'&#'#$&%#$$#$##$","+1#(,#('#(#$'&#$%#$$#$##$","*0#)*#)&%'(#%&#%#&&##&","*/#*(#*#%(&#%$#%#$$##$","*.#+&#+#(&#%&$#%#$$##$","*-#,)('%('(#(#*%#(%##(","*,#-()'(%'*#%(#%#((##(","*+#.#&+(#&%#&#$%$#$##$","**#/#(*%#(#&%#$%$#$##$","*)#0#*)%&'&#&#(%#&%##&","*/**/#*')+)#)#-'#)'##)","*-),0#)-&&-#&#(-(#(##(","*-*,/#*.)$-)$#)-)#)##)",",*(/1#(,#(*&%#-*#&*)#&&#&##&","*+*./#*#-+(*&(#*#((##(","","",",4#&1#&.#&+#&(#&%#&#$%$#$##$","(3#'/#'+#''#'##'","'2#(-#((#(##(",")1#)+#)%#)#'%#%%##%","*0#*)#*%&'&#&#(%#&%##&","'/#+'#+#''##'","+.#,%#,#*%#(%#&%#$%$#$##$","%-#-##-",
"+,#.#%,*#%(#%&#%$#%#$$##$","'+#/#'+'#'##'","**#0#)*&%'(#%&#%#&&##&","))#1#+)#%)'#%%#%##%","'(#2#-(#((##(","('#3#/'#+'#''##'","*.+,/#+.*$.)$#).)#)##)",")-+-/#+#+-'#+#''##'",",('23#'/#'+#'#1(#,(#'('#'##'","","","*5#&2#&/#&,#&)#&&#&##&",",4#'0#',#'(#'$#'#&$#%$#$$##$","+3#(.#()#(&%&'#%#%&%#%##%","(2#),#)&#)#&&##&","&1#**#*##*","*0#+(#+#&(%#&#$%$#$##$","(/#,&#,#)&#&&##&","*.#-)(()#(#')%#'#%%##%","*-#.()()%'+#%)#%#)(##)","(,#/#&,)#&&#&##&","*+#0#(+&#(#%&$#%#$$##$","&*#1#**##*","()#2#,)#&)&#&##&","+(#3#.(#)(%&&%#&#'%#%%##%",",'#4#0'#,'#('#$'&#$%#$$#$##$","(/,,/#,#)/)#)##)","*.,-/#,.+$#+.'#+#''##'","+*)12#),#)#0*#)*&#)#&&##&","",
"","-6#&3#&0#&-#&*#&'#&$#&#%$#$$##$","*5#'1#'-#')#'%#'#%%##%","+4#(/#(*#(%#(#&%#$%$#$##$",")3#)-#)'#)#%'%#%##%",",2#*+#*'&'(#&'%$#&'&%$&#%##&",")1#+)#+#%)'#%%#%##%","+0#,'#,#('#$'&#$%#$$#$##$",")/#-)')+#'#')'#'##'","%.#.##.",")-#/'))'#)#+'#''##'","+,#0#',(#'$#'#&$#%$#$$##$",")+#1#)+%#)#'%#%%##%","+/(-4#(/#(#&/,#&)#&&#&##&","))#3#-)#')%#'#%%##%","+(#4#/(#*(#%(&#%$#%#$$##$","*'#5#1'#-'#)'#%'%#%##%","+.+.1#+/)%#+.-)%+)%+#)##+",")/--/#-#+/'#+#''##'","+.-./#-#-.)')+#'#')'#'##'","","","-7#&4#&1#&.#&+#&(#&%#&#$%$#$##$",",6#'2#'.#'*#'&#'#$&%#$$#$##$","+5#(0#(+#(&#(#%&$#%#$$##$","+4#).#)(#)%&&%#&#'%#%%##%","+3#*,#*%#*#(%#&%#$%$#$##$",",2#+*#+&''&#'#(&#%&$#%#$$##$","+1#,(#,#'($#'#&$#%$#$$##$","+0#-&#-#*&#'&#$&%#$$#$##$",
"+/#.'&+,#&)#&#*'#&'&#&##&","+.#/&'+*#'&#'#,&#)&#&&##&","+-#0#&-*#&'#&$#&#%$#$$##$","+,#1#(,'#(#$'&#$%#$$#$##$","+1),4#)(),.#)(#)#-(#((##(","+*#3#,*#%*(#%&#%$#%#$$##$","+)#4#.)#()&%&'#%#%&%#%##%","+(#5#0(#+(#&(%#&#$%$#$##$",",'#6#2'#.'#*'#&'$#&#%$#$$##$","++(25#(0#(+#(#/+#'+'#'##'","+,*13#*,#*#/,#&,)#&&#&##&","+/../#.#-/)')+#'#')'#'##'","","","+8#&5#&2#&/#&,#&)#&&#&##&",")7#'3#'/#'+#''#'##'",",6#(1#(,#('#(#$'&#$%#$$#$##$","'5#)/#))#)##)","+4#*-#*&#*#'&#$&%#$$#$##$","&3#++#+##+","(2#,)#,#&)&#&##&",")1#-'#-#)'#%'%#%##%","*0#.+)('*'*)$*#)#*'##*","%/#/##/","*.#0)+(*''*#')*$#*)##*",")-#1#'-)#'%#'#%%##%","(,#2#),&#)#&&##&","&+#3#++##+","+*#4#-*#&*'#&$#&#%$#$$##$","')#5#/)#))##)",
",(#6#1(#,(#'($#'#&$#%$#$$##$","(/+/3#+#+/+#+##+","*/,/2#,/)&#,/,)&,#)##,","*+)35#)/#)#1+#)+)#)##)","+,+23#+#1,&+)+#+#.&#+&##+","","",".9#&6#&3#&0#&-#&*#&'#&$#&#%$#$$##$","-8#'4#'0#',#'(#'$#'#&$#%$#$$##$","(7#(2#(-#((#(##(","+6#)0#)*#)&%'(#%&#%#&&##&","+5#*.#*'#*#&'$#&#%$#$$##$",",4#+,#+'&()#&'$%(#$'#$#''##'","+3#,*#,#%*(#%&#%$#%#$$##$","'2#-(#-#((##(","+1#.&#.#+&#(&#%&$#%#$$##$","+0#/'&,-#&*#&'#&#+'#''##'","+/#0&',+#''#'#-&#*&#'&##'","+.#1#&.+#&(#&%#&#$%$#$##$","'-#2#(-(#(##(","+,#3#*,%#*#(%#&%#$%$#$##$",",+#4#,+&'('#'#)&$'%#($#'$##'","+*#5#.*#'*&#'#$&%#$$#$##$","+)#6#0)#*)%&'&#&#(%#&%##&","((#7#2(#-(#((##(","+0,/3#,2+$1+$0+$#+0+#+##+","+1..1#.#+1)#+#%)'#%%#%##%","++)46#)0#)#2+#*+*)$*#)##*","+,+34#+,#+#2,#),&#)#&&##&","",
"",".:#&7#&4#&1#&.#&+#&(#&%#&#$%$#$##$","+9#'5#'1#'-#')#'%#'#%%##%",",8#(3#(.#()#(&%&'#%#%&%#%##%","*7#)1#)+#)%#)#'%#%%##%","+6#*/#*(#*#%(&#%$#%#$$##$","*5#+-#+%#+#)%#'%#%%##%",",4#,+#,&'('#'#)&$'%#($#'$##'",")3#-)#-#')%#'#%%##%","+2#.'#.#*'#&'$#&#%$#$$##$",")1#/+))+#)#'+'#'##'","%0#0##0",")/#1)+)+''+#'#+)##+","+.#2#'.*#'&#'#$&%#$$#$##$",")-#3#)-'#)#%'%#%##%",",,#4#+,'&()#&'$%(#$'#$#''##'","*+#5#-+#%+)#%'#%%#%##%","+*#6#/*#(*%#(#&%#$%$#$##$","*)#7#1)#+)#%)'#%%#%##%","+1,/4#,1)&1&&1#&#*1*#*##*",")1-/3#-1+%#+1+#+##+","+0-03#-1+%1)%#-0-)'-#)##-","*+)57#)1#)+#)#3+#++##+","+0/01#/#/0)'+-#')#'#))##)","","",",;#&8#&5#&2#&/#&,#&)#&&#&##&","-:#'6#'2#'.#'*#'&#'#$&%#$$#$##$",",9#(4#(/#(*#(%#(#&%#$%$#$##$",")8#)2#),#)&#)#&&##&",
"+7#*0#*)#*%&'&#&#(%#&%##&","+6#+.#+&#+#(&#%&$#%#$$##$","&5#,,#,##,","+4#-*#-#&*'#&$#&#%$#$$##$","+3#.(#.#)(%&&%#&#'%#%%##%",")2#/&#/#,&#)&#&&##&","+1#0*)*+#)#)*%#)#'%#%%##%","+0#1*+)*%).#%,#%*#%#**##*",")/#2#&/,#&)#&&#&##&","+.#3#(.)#(&%&'#%#%&%#%##%","+-#4#*-&#*#'&#$&%#$$#$##$","&,#5#,,##,","++#6#.+#&+(#&%#&#$%$#$##$","+*#7#0*#)*&%'(#%&#%#&&##&","))#8#2)#,)#&)&#&##&","+3..3#.#)3-#)'#)#%'%#%##%","+2./3#.2-$2,$2+$#+2+#+##+","*2//2#/#,2)#,#&)&#&##&","-1/08))8#)1(*3#(#.1.+&.(&.#(##.","+1001#0#/1)'+-#')#'#))##)","","","/<#&9#&6#&3#&0#&-#&*#&'#&$#&#%$#$$##$","*;#'7#'3#'/#'+#''#'##'",",:#(5#(0#(+#(&#(#%&$#%#$$##$","*9#)3#)-#)'#)#%'%#%##%","'8#*1#**#*##*","(7#+/#+'#+#''##'","+6#,-#,('()#'#'(%#'#%%##%","*5#-+#-#%+)#%'#%%#%##%",
"+4#.)#.#()&%&'#%#%&%#%##%","(3#/'#/#+'#''##'",",2#0(&-/#&,#&)#&#+(#&(&#&##&","%1#1##1","+6),9#)-),3#)-#)#(-(#(##(","(/#3#'/+#''#'##'","+.#4#).(#)%&&%#&#'%#%%##%","*-#5#+-%#+#)%#'%#%%##%","+,#6#-,'(('#(#)'#%'%#%##%","(+#7#/+#'+'#'##'","'*#8#1*#**##*","*)#9#3)#-)#')%#'#%%##%",",(#:#5(#0(#+(#&(%#&#$%$#$##$","(3//3#/#+3+#+##+","-2/03#/2.$2-$#-2)#-#')%#'#%%##%","*1/13#/#/1'#/#+'#''##'","+.-45#-#3.+0&+-&+#-#++##+","","","/=#&:#&7#&4#&1#&.#&+#&(#&%#&#$%$#$##$",".<#'8#'4#'0#',#'(#'$#'#&$#%$#$$##$","-;#(6#(1#(,#('#(#$'&#$%#$$#$##$",",:#)4#).#)(#)%&&%#&#'%#%%##%","-9#*2#*+#*'&'(#&'%$#&'&%$&#%##&","+8#+0#+(#+#&(%#&#$%$#$##$",",7#,.#,%#,#*%#(%#&%#$%$#$##$","+6#-,#-'(('#(#)'#%'%#%##%","+5#.*#.#'*&#'#$&%#$$#$##$","+4#/(#/#*(#%(&#%$#%#$$##$",",3#0�#-&#*&#'&#$&%#$$#$##$",
"+2#1+**+#*#)+%#)#'%#%%##%","+1#2)*+*#*#,)'*%%*%#*%##*",",0#3#&0-#&*#&'#&$#&#%$#$$##$","+/#4#(/*#(%#(#&%#$%$#$##$","+.#5#*.'#*#&'$#&#%$#$$##$","+-#6#,-('()#'#'(%#'#%%##%",",,#7#.,#%,*#%(#%&#%$#%#$$##$","++#8#0+#(+&#(#%&$#%#$$##$",",5..5#.#'51#'-#')#'%#'#%%##%",",)#:#4)#.)#()&%&'#%#%&%#%##%","-(#;#6(#1(#,(#'($#'#&$#%$#$$##$","-2.15#.2+&#-20+%.+%-,$-+$-#+##-","+3003#0#-3)#-#')%#'#%%##%","+2013#02/$#/2'#/#+'#''##'",",+*89#*2#*+#*#7+#/+#'+'#'##'","","","->#&;#&8#&5#&2#&/#&,#&)#&&#&##&",",=#'9#'5#'1#'-#')#'%#'#%%##%",")<#(7#(2#(-#((#(##(","(;#)5#)/#))#)##)",",:#*3#*,#*%#*#(%#&%#$%$#$##$","*9#+1#+)#+#%)'#%%#%##%",")8#,/#,&#,#)&#&&##&","&7#--#-##-","+6#.+#.#&+(#&%#&#$%$#$##$","'5#/)#/#))##)",",4#0'#0#,'#('#$'&#$%#$$#$##$","+3#1+)+-#)+'%#)+)'%)#'##)","%2#2##2",
"+1#3)++)#+#-)#')%#'#%%##%",",0#4#'0,#'(#'$#'#&$#%$#$$##$","'/#5#)/)#)##)","+.#6#+.&#+#(&#%&$#%#$$##$","&-#7#--##-","),#8#/,#&,)#&&#&##&","*+#9#1+#)+%#)#'%#%%##%",",*#:#3*#,*#%*(#%&#%$#%#$$##$","()#;#5)#/)#))##)","(2-27#-#-2-#-##-","+-)7;#)5#)/#)#3-#)-)#)##)",")2/25#/#/2)#/#))##)","*3113#1#/3'#/#+'#''##'",",-,78#,/#,#6-#,-&#,#)&#&&##&","","","0?#&<#&9#&6#&3#&0#&-#&*#&'#&$#&#%$#$$##$",".>#':#'6#'2#'.#'*#'&#'#$&%#$$#$##$","-=#(8#(3#(.#()#(&%&'#%#%&%#%##%",",<#)6#)0#)*#)&%'(#%&#%#&&##&",",;#*4#*-#*&#*#'&#$&%#$$#$##$","-:#+2#+*#+&''&#'#(&#%&$#%#$$##$",",9#,0#,'#,#('#$'&#$%#$$#$##$","+8#-.#-(')*#'(%%(#%#((##(",",7#.,#.#%,*#%(#%&#%$#%#$$##$","+6#/*#/#(*%#(#&%#$%$#$##$","+5#0(#0#+(#&(%#&#$%$#$##$","+4#1-**-#*#'-)#'%#'#%%##%","+3#2)(-.#()#(#,)#&)&#&##&","+2#3()-,#))&&)#&#.(#)(##)",
"+1#4*-*-)'-%'/#%-#%#-*##-","+0#5#(0+#(&#(#%&$#%#$$##$","+/#6#*/(#*#%(&#%$#%#$$##$",",.#7#,.%#,#*%#(%#&%#$%$#$##$","+-#8#.-'()(#(#*'%(%#(%##(","+7..7#.+-/-#-#1+'-'#-'##-","+6./7#.*./,#.*,%#3*#,*##,","+3,29#,3&)6#&3#&#+3+#+##+","+4.17#.4+&#+4/#+'#+#''##'","+3.27#.+5+,.*,#.#5+#,,##,","-3/26#/4-%4+%3.$#.31+&.+&.#+##.","+3025#04/$3/$#/3)#/#))##)","+/-68#-#4/).).-$.#-#.)##.","+1045#01,'#31*,*,#,#,*##,","","","0@#&=#&:#&7#&4#&1#&.#&+#&(#&%#&#$%$#$##$","+?#';#'7#'3#'/#'+#''#'##'","->#(9#(4#(/#(*#(%#(#&%#$%$#$##$","+=#)7#)1#)+#)%#)#'%#%%##%",",<#*5#*.#*'#*#&'$#&#%$#$$##$","';#+3#++#+##+",",:#,1#,(#,#'($#'#&$#%$#$$##$","*9#-/#-)')+#'#')'#'##'","+8#.-#.'()(#(#*'%(%#(%##(","(7#/+#/#'+'#'##'","+6#0)#0#*)%&'&#&#(%#&%##&","*5#1'#1#-'#)'#%'%#%##%",",4#2-+*',),+$,#+#.'%,%#,%##,","%3#3##3",
",2#4+-*,').#',%%,#%+,$#,+##,","*1#5#'1-#')#'%#'#%%##%","+0#6#)0*#)&%'(#%&#%#&&##&","(/#7#+/'#+#''##'","+.#8#-.(')*#'(%%(#%#((##(","*-#9#/-'))'#)#+'#''##'",",,#:#1,#(,'#(#$'&#$%#$$#$##$","'+#;#3+#++##+",",*#<#5*#.*#'*&#'#$&%#$$#$##$","+)#=#7)#1)#+)#%)'#%%#%##%","+4/27#/5-%4.$4-$#-4-#-##-","*3/37#/3+'#/3/+'/#+##/","+4125#140$4/$#/4)#/#))##)","*/-79#-/#-#5/#)/)#)##)",",0/67#/0(*2#(#50#(0-#((#(##(","","",".A#&>#&;#&8#&5#&2#&/#&,#&)#&&#&##&","/@#'<#'8#'4#'0#',#'(#'$#'#&$#%$#$$##$","-?#(:#(5#(0#(+#(&#(#%&$#%#$$##$","*>#)8#)2#),#)&#)#&&##&",",=#*6#*/#*(#*#%(&#%$#%#$$##$","-<#+4#+,#+'&()#&'$%(#$'#$#''##'",");#,2#,)#,#&)&#&##&",",:#-0#-&#-#*&#'&#$&%#$$#$##$","&9#..#.##.",")8#/,#/#&,)#&&#&##&","+7#0*#0#)*&%'(#%&#%#&&##&","+6#1/**/#*')+)#)#-'#)'##)",")5#2,),/#)#),)#)##)",
",4#3*)-.#)#,*')&(#)'($#('##(",",3#4)*-,#*)'&#.)#()('$(#'##(",")2#5),,)#,#/)#))##)","+1#6*/*+))+#)#/*#'+'#'##'","+0#7#*0)#*%&'&#&#(%#&%##&",")/#8#,/&#,#)&#&&##&","&.#9#..##.",",-#:#0-#&-*#&'#&$#&#%$#$$##$","),#;#2,#),&#)#&&##&","-+#<#4+#,+&'('#'#)&$'%#($#'$##'","+4-3:#-5((5#(4,$#,4,#,##,","*)#>#8)#2)#,)#&)&#&##&","+5027#05.%6-$5-$#-5-#-##-",",2.59#.)7,).,.#.#:)#4)#.)##.",")5225#2#/5)#/#))##)",",.,9;#,2#,/).#,.,)&,#)##,",",2156#12-'#42+-*,#-+,$#,+##,","","","1B#&?#&<#&9#&6#&3#&0#&-#&*#&'#&$#&#%$#$$##$","-A#'=#'9#'5#'1#'-#')#'%#'#%%##%",".@#(;#(6#(1#(,#('#(#$'&#$%#$$#$##$","+?#)9#)3#)-#)'#)#%'%#%##%",",>#*7#*0#*)#*%&'&#&#(%#&%##&","+=#+5#+-#+%#+#)%#'%#%%##%",",<#,3#,*#,#%*(#%&#%$#%#$$##$","*;#-1#-'#-#)'#%'%#%##%",",:#./#.'&+,#&)#&#*'#&'&#&##&","*9#/-#/'))'#)#+'#''##'","+8#0+#0#(+&#(#%&$#%#$$##$",
"*7#1)#1#+)#%)'#%%#%##%","+6#2-),0#)-&&-#&#(-(#(##(","+5#3-++-#+#)-'#)#%'%#%##%","%4#4##4","+3#5+-+-')/#'-%%-#%#-+##-","+2#6)-,-((-#(#0)&-&#-&##-","*1#7#)1+#)%#)#'%#%%##%","+0#8#+0(#+#&(%#&#$%$#$##$","*/#9#-/)')+#'#')'#'##'",",.#:#/.&'+*#'&#'#,&#)&#&&##&","*-#;#1-#'-)#'%#'#%%##%","+8/09#/8.$*.1.#.#5*#.*##.","++#=#5+#-+#%+)#%'#%%#%##%",",*#>#7*#0*#)*&%'(#%&#%#&&##&","*7117#1#+7/#+'#+#''##'",",6127#160$6/$6.$6-$#-6-#-##-","+5137#15/%#/5+#/#'+'#'##'",",4147#15/%#143/%1/%1))1#)##1","+1/79#/#51+/)-#/+-%#-+##-",",/.9:#./#.#8/#,/&#,#)&#&&##&","","","1C#&@#&=#&:#&7#&4#&1#&.#&+#&(#&%#&#$%$#$##$","/B#'>#':#'6#'2#'.#'*#'&#'#$&%#$$#$##$","*A#(<#(7#(2#(-#((#(##(","-@#):#)4#).#)(#)%&&%#&#'%#%%##%","(?#*8#*1#**#*##*",",>#+6#+.#+&#+#(&#%&$#%#$$##$","-=#,4#,+#,&'('#'#)&$'%#($#'$##'","(<#-2#-(#-#((##(",
"+;#.0#.)'*,#'#()('$(#'##(",",:#/.#/&'+*#'&#'#,&#)&#&&##&",",9#0,#0#',(#'$#'#&$#%$#$$##$","'8#1*#1#**##*","(7#2(#2#-(#((##(","+6#3-*,/#*.)$-)$#)-)#)##)",",5#4,+,-#+#+,%#+#)%#'%#%%##%",",4#5,-+,%+2#%0#%.#%,#%#,,##,","+3#6*-,#/*).$)-$)#-#))##)","(2#7#(2-#((#(##(","'1#8#*1*#*##*",",0#9#,0'#,#('#$'&#$%#$$#$##$",",/#:#./'&+,#&)#&#*'#&'&#&##&","+.#;#0.')*(#)'($#,'#('##(","(-#<#2-#(-(#(##(","+9009#0+/1-#/+-%#5+#-+##-",",+#>#6+#.+#&+(#&%#&#$%$#$##$","(*#?#8*#1*#**##*",",7128#1(12*#1#;(#6(#1(#**##*","(7227#2#-7-#-##-","+5148#15.&5+2+(0#+##0","-6336#3#06)#0#*)%&'&#&#(%#&%##&",",.,;=#,4#,.&)1#&.#	.#..##.","+3267#23.'#53,.*,#.#,,##,","","","/D#&A#&>#&;#&8#&5#&2#&/#&,#&)#&&#&##&",",C#'?#';#'7#'3#'/#'+#''#'##'",".B#(=#(8#(3#(.#()#(&%&'#%#%&%#%##%",")A#);#)5#)/#))#)##)",
".@#*9#*2#*+#*'&'(#&'%$#&'&%$&#%##&",")?#+7#+/#+'#+#''##'","'>#,5#,,#,##,","*=#-3#-)#-#')%#'#%%##%",",<#.1#.&#.#+&#(&#%&$#%#$$##$","&;#//#/##/",",:#0-#0#&-*#&'#&$#&#%$#$$##$","*9#1+#1#)+%#)#'%#%%##%",")8#2)#2#,)#&)&#&##&",")7#3'#3#/'#+'#''##'","-6#4*(/1#(,#(*&%#-*#&*)#&&#&##&","%5#5##5","-4#6(*/-#*#1(#,(&*%&#*#)&#&&##&",")3#7#'3/#'+#''#'##'",")2#8#)2,#)&#)#&&##&","*1#9#+1)#+#%)'#%%#%##%",",0#:#-0&#-#*&#'&#$&%#$$#$##$","&/#;#//##/",",.#<#1.#&.+#&(#&%#&#$%$#$##$","*-#=#3-#)-'#)#%'%#%##%","',#>#5,#,,##,",")+#?#7+#/+#'+'#'##'","-703C,'?,';,'>#,7,'#,75#,,#,##,","(5/5;#/#/5/#/##/","-6149#16.&6+&6(&#/6/(*4#(/#(##/","*7337#3#/7+#/#'+'#'##'","*/,;>#,5#,#8/#,/,#,##,","+5357#3#35'#3#/'#+'#''##'",",2189#12**2#*#72#(2-#((#(##(","",
"","2E#&B#&?#&<#&9#&6#&3#&0#&-#&*#&'#&$#&#%$#$$##$","0D#'@#'<#'8#'4#'0#',#'(#'$#'#&$#%$#$$##$",".C#(>#(9#(4#(/#(*#(%#(#&%#$%$#$##$","-B#)<#)6#)0#)*#)&%'(#%&#%#&&##&","-A#*:#*3#*,#*%#*#(%#&%#$%$#$##$",",@#+8#+0#+(#+#&(%#&#$%$#$##$",",?#,6#,-#,('()#'#'(%#'#%%##%",",>#-4#-*#-#&*'#&$#&#%$#$$##$",",=#.2#.'#.#*'#&'$#&#%$#$$##$",",<#/0#/'&,-#&*#&'#&#+'#''##'","+;#0.#0')*(#)'($#,'#('##(",",:#1,#1#(,'#(#$'&#$%#$$#$##$",",9#2/(-4#(/#(#&/,#&)#&&#&##&",",8#3(#3#.(#)(%&&%#&#'%#%%##%","+7#4/,+).).-$.,$.#,#.)##.","+6#5+*./#*#-+(*&(#*#((##(","+5#6*+.-#+*(&#/*#(*(#(##(","+4#7,/+.)).#)-.$,.$#.,##.",",3#8#(3.#()#(&%&'#%#%&%#%##%","+=..=#./+15#+#-/-+%-#+##-",",1#:#,1(#,#'($#'#&$#%$#$$##$","+0#;#.0)'*,#'#()('$(#'##(",",/#<#0/&',+#''#'#-&#*&#'&##'",",.#=#2.#'.*#'&#'#$&%#$$#$##$",",-#>#4-#*-&#*#'&#$&%#$$#$##$",",,#?#6,#-,'(('#(#)'#%'%#%##%","+7/4<#/7*(#,75*%5#*,#,##,",",9229#2#+91#+)#+#%)'#%%#%##%","-)#B#<)#6)#0)#*)%&'&#&#(%#&%##&",
"+615:#16-'#063-&0-&0#-##0",",2.9=#.2#.#52),,)#,#/)#))##)",",7447#4#17)#1#+)#%)'#%%#%##%",",536D/'D+'D''D#'#4543$4#3##4",",10:;#06+(1+(3#+#91#+1+#+##+","","","2F#&C#&@#&=#&:#&7#&4#&1#&.#&+#&(#&%#&#$%$#$##$",".E#'A#'=#'9#'5#'1#'-#')#'%#'#%%##%",".D#(?#(:#(5#(0#(+#(&#(#%&$#%#$$##$",",C#)=#)7#)1#)+#)%#)#'%#%%##%","-B#*;#*4#*-#*&#*#'&#$&%#$$#$##$","+A#+9#+1#+)#+#%)'#%%#%##%","-@#,7#,.#,%#,#*%#(%#&%#$%$#$##$","+?#-5#-+#-#%+)#%'#%%#%##%",",>#.3#.(#.#)(%&&%#&#'%#%%##%","*=#/1#/)'+-#')#'#))##)",",<#0/#0&',+#''#'#-&#*&#'&##'","*;#1-#1#'-)#'%#'#%%##%",",:#21),4#)(),.#)(#)#-(#((##(","*9#3)#3#-)#')%#'#%%##%","-8#4'#4#0'#,'#('#$'&#$%#$$#$##$","*7#5-+-/#+#+-'#+#''##'","%6#6##6","*5#7+--+#-#/+#'+'#'##'","-4#8#'40#',#'(#'$#'#&$#%$#$$##$","*3#9#)3-#)'#)#%'%#%##%",",2#:)1,)(,-#(#4)#.)#()(#(##(","*1#;#-1'#-#)'#%'%#%##%",",0#<#/0'&,-#&*#&'#&#+'#''##'",
"*/#=#1/')+)#)#-'#)'##)",",.#>#3.#(.)#(&%&'#%#%&%#%##%","*;11;#1+/3/#/#7+#/+##/","-,#@#7,#.,#%,*#%(#%&#%$#%#$$##$","*7/5=#/7))7#)#-7-#-##-",",6/6=#/7))7#)#/6+#/#'+'#'##'","*715;#19/%7/%#/7/#/##/",",616;#17-'#163-'1/%1-%1#-##1",",1-;?#-5#-1)'#71#)1/#))#)##)",",6369#371%7/%#363/'3))3#)##3","*319;#1#73-1)-#1#--##-",",656#567#5-+-/#+#+-'#+#''##'","","","0G#&D#&A#&>#&;#&8#&5#&2#&/#&,#&)#&&#&##&","0F#'B#'>#':#'6#'2#'.#'*#'&#'#$&%#$$#$##$","/E#(@#(;#(6#(1#(,#('#(#$'&#$%#$$#$##$","+D#)>#)8#)2#),#)&#)#&&##&","-C#*<#*5#*.#*'#*#&'$#&#%$#$$##$",".B#+:#+2#+*#+&''&#'#(&#%&$#%#$$##$","*A#,8#,/#,&#,#)&#&&##&",",@#-6#-,#-'(('#(#)'#%'%#%##%",",?#.4#.)#.#()&%&'#%#%&%#%##%","*>#/2#/&#/#,&#)&#&&##&","&=#00#0##0",",<#1.#1#&.+#&(#&%#&#$%$#$##$",");#2,#2#),&#)#&&##&",",:#3*#3#,*#%*(#%&#%$#%#$$##$",",9#4(#4#/(#*(#%(&#%$#%#$$##$",")8#5/,,/#,#)/)#)##)",
"-7#6('23#'/#'+#'#1(#,(#'('#'##'",",>+/B#+2+/:#+2#+#(2-#((#(##(",")5#8,/,/))/#)#/,##/",",4#9#(4/#(*#(%#(#&%#$%$#$##$",",3#:#*3,#*%#*#(%#&%#$%$#$##$",")2#;#,2)#,#&)&#&##&",",1#<#.1&#.#+&#(&#%&$#%#$$##$","&0#=#00##0","*/#>#2/#&/,#&)#&&#&##&",",.#?#4.#).(#)%&&%#&#'%#%%##%",",-#@#6-#,-('()#'#'(%#'#%%##%","*,#A#8,#/,#&,)#&&#&##&",",805=#0,6/20),0)0#0#9,#0,##0","-*#C#<*#5*#.*#'*&#'#$&%#$$#$##$",")825;#28/&#/8/#/##/",",9449#4#/9-#/'))'#)#+'#''##'",",1-<@#-6#-1((1#(#81#*1*#*##*","*/,>A#,8#,/#,#;/#//##/",",20;=#0#92)0,0#0#3)&0�&##0",",7667#6#57-+-/#+#+-'#+#''##'","","","3H#&E#&B#&?#&<#&9#&6#&3#&0#&-#&*#&'#&$#&#%$#$$##$","-G#'C#'?#';#'7#'3#'/#'+#''#'##'","+F#(A#(<#(7#(2#(-#((#(##(",",E#)?#)9#)3#)-#)'#)#%'%#%##%","-D#*=#*6#*/#*(#*#%(&#%$#%#$$##$","(C#+;#+3#++#+##+","-B#,9#,0#,'#,#('#$'&#$%#$$#$##$","'A#-7#--#-##-",
",@#.5#.*#.#'*&#'#$&%#$$#$##$",")?#/3#/'#/#+'#''##'",",>#07)*8#)0)*2#)0'%0%%0#%##0","*=#1/#1')+)#)#-'#)'##)","(<#2-#2#(-(#(##(","';#3+#3#++##+",",:#4)#4#.)#()&%&'#%#%&%#%##%","+9#5'#5#1'#-'#)'#%'%#%##%","+8#6/-,'.+.-$.#-#2'#.'##.","%7#7##7","+6#8-/,.'+2#'.#'-.$#.-##.","+5#9#'51#'-#')#'%#'#%%##%",",4#:#)4.#)(#)%&&%#&#'%#%%##%","'3#;#+3+#+##+","(2#<#-2(#-#((##(","*1#=#/1)'+-#')#'#))##)",",0#>*8)*2).0%,0%*0%#7*#0*##0",")/#?#3/#'/+#''#'##'","+;03>#0;-&/4/4-*4#-#4/##4","'-#A#7-#--##-",",;23<#2+23-#2#:+#2+#(-(#(##(","(+#C#;+#3+#++##+",",925B),E#)9),?#)9#)#.9.#.##.","*935;#391%9/%#/9/#/##/","*727<#27-(#272-(2#-##2",")737;#3#37+#3#++##+",",1.=@#.5#.3,%1,%#:1#,1,#,##,",",-+AC#+;#+3#+#?-#5-#+-+#+##+",",32;<#27-(#:3+2+2-(2#-#2+##2","",
"","3I#&F#&C#&@#&=#&:#&7#&4#&1#&.#&+#&(#&%#&#$%$#$##$","1H#'D#'@#'<#'8#'4#'0#',#'(#'$#'#&$#%$#$$##$","/G#(B#(=#(8#(3#(.#()#(&%&'#%#%&%#%##%",".F#)@#):#)4#).#)(#)%&&%#&#'%#%%##%","-E#*>#*7#*0#*)#*%&'&#&#(%#&%##&",".D#+<#+4#+,#+'&()#&'$%(#$'#$#''##'","-C#,:#,1#,(#,#'($#'#&$#%$#$$##$",",B#-8#-.#-(')*#'(%%(#%#((##(",",A#.6#.+#.#&+(#&%#&#$%$#$##$",",@#/4#/(#/#*(#%(&#%$#%#$$##$","-?#02#0(&-/#&,#&)#&#+(#&(&#&##&",",>#17**7#*)#1#+)#%)'#%%#%##%",",=#2.#2#'.*#'&#'#$&%#$$#$##$",",<#3,#3#*,%#*#(%#&%#$%$#$##$",",;#4*#4#-*#&*'#&$#&#%$#$$##$",",:#5(#5#0(#+(#&(%#&#$%$#$##$",",9#6.+.1#+/)%#+.-)%+)%+#)##+",",8#7*)12#),#)#0*#)*&#)#&&##&",",7#8)*10#*)#*#2)#,)#&)&#&##&",",6#9+..+#.#1+#)+%#)#'%#%%##%",",5#:#(50#(+#(&#(#%&$#%#$$##$",",4#;#*4-#*&#*#'&#$&%#$$#$##$",",3#<#,3*#,#%*(#%&#%$#%#$$##$",",2#=#.2'#.#*'#&'$#&#%$#$$##$",",1#>*7*+1)#7*%1)#5%#3%#1%##1",",8+7D#+<#+8''8#'#*81#**#*##*",",/#@#4/#(/*#(%#(#&%#$%$#$##$",",.#A#6.#+.&#+#(&#%&$#%#$$##$",",-#B#8-#.-'()(#(#*'%(%#(%##(",
",;24=#2*24.#2*.'#<*#5*#.*##.",",:25=#2.8/42).2).#2#9.#..##.",",;44;#4#-;1#-'#-#)'#%'%#%##%",",827=#28-(8((8#(#18*#1#**##*",".:55:#5#0:-#0#&-*#&'#&$#&#%$#$$##$",",738D++D#+#4763$53$43$4#3##4",",9669#6#39)#3#-)#')%#'#%%##%",",20=?#02#0#;2#,2)#,#&)&#&##&",",32<=#23(-8#(3#(#;3#+3+#+##+","","","1J#&G#&D#&A#&>#&;#&8#&5#&2#&/#&,#&)#&&#&##&","/I#'E#'A#'=#'9#'5#'1#'-#')#'%#'#%%##%","/H#(C#(>#(9#(4#(/#(*#(%#(#&%#$%$#$##$","*G#)A#);#)5#)/#))#)##)",")F#*?#*8#*1#**#*##*",",E#+=#+5#+-#+%#+#)%#'%#%%##%","*D#,;#,2#,)#,#&)&#&##&","+C#-9#-/#-)')+#'#')'#'##'","-B#.7#.,#.#%,*#%(#%&#%$#%#$$##$","(A#/5#/)#/#))##)","-@#03#0�#-&#*&#'&#$&%#$$#$##$","&?#11#1##1","*>#2/#2#&/,#&)#&&#&##&","*=#3-#3#)-'#)#%'%#%##%","-<#4+#4#,+&'('#'#)&$'%#($#'$##'","(;#5)#5#/)#))##)","-:#6'#6#2'#.'#*'#&'$#&#%$#$$##$","*9#7/--/#-#+/'#+#''##'","%8#8##8",
"*7#9-/-/'+3#'/#'#/-##/","-6#:#'62#'.#'*#'&#'#$&%#$$#$##$","(5#;#)5/#))#)##)","-4#<#+4,#+'&()#&'$%(#$'#$#''##'","*3#=#-3)#-#')%#'#%%##%","*2#>#/2&#/#,&#)&#&&##&","&1#?#11##1","-0#@#30#&0-#&*#&'#&$#&#%$#$$##$","(/#A#5/#)/)#)##)","-.#B#7.#,.%#,#*%#(%#&%#$%$#$##$","+-#C#9-#/-'))'#)#+'#''##'","*,#D#;,#2,#),&#)#&&##&",",+#E#=+#5+#-+#%+)#%'#%%#%##%","(818?#1#181#1##1","(;55;#5#/;/#/##/",",838=#39/';-%9-%#383-)3#-##3","*957;#593%#39+#3#++##+","*858;#5#58)#5#/)#))##)","+1/?A#/5#/#=1#/1)#/#))##)",",878#789#7-+/1#+-''-#'#--##-","","","4K#&H#&E#&B#&?#&<#&9#&6#&3#&0#&-#&*#&'#&$#&#%$#$$##$","1J#'F#'B#'>#':#'6#'2#'.#'*#'&#'#$&%#$$#$##$","/I#(D#(?#(:#(5#(0#(+#(&#(#%&$#%#$$##$",".H#)B#)<#)6#)0#)*#)&%'(#%&#%#&&##&","/G#*@#*9#*2#*+#*'&'(#&'%$#&'&%$&#%##&","-F#+>#+6#+.#+&#+#(&#%&$#%#$$##$","-E#,<#,3#,*#,#%*(#%&#%$#%#$$##$","-D#-:#-0#-&#-#*&#'&#$&%#$$#$##$",
",C#.8#.-#.'()(#(#*'%(%#(%##(",",B#/6#/*#/#(*%#(#&%#$%$#$##$","-A#04#0'#0#,'#('#$'&#$%#$$#$##$",",@#19**9#*+#1#)+%#)#'%#%%##%",",?#26),9#)-),3#)-#)#(-(#(##(",",>#3.#3#(.)#(&%&'#%#%&%#%##%","-=#4,#4#+,'&()#&'$%(#$'#$#''##'",",<#5*#5#.*#'*&#'#$&%#$$#$##$","-;#6(#6#1(#,(#'($#'#&$#%$#$$##$",",:#7+(25#(0#(+#(#/+#'+'#'##'",",9#8.-./#-#-.)')+#'#')'#'##'",",8#9./-2))2#).+'.''.#'#..##.",",7#:(+2/#++''+#'#5(#0(#+(##+",",A.0C#.4.08#.4*'#*41#**#*##*",",5#<#*5.#*'#*#&'$#&#%$#$$##$","-4#=#,4+#,&'('#'#)&$'%#($#'$##'",",3#>#.3(#.#)(%&&%#&#'%#%%##%",",2#?)6,)-,-((-#(#9)#3)#-)##-",",1#@*9*+3)/1%-1%+1%#9*#1+##1",",?22?#2-/53#/-))-#)#7-#--##-",",/#B#6/#*/(#*#%(&#%$#%#$$##$",",.#C#8.#-.(')*#'(%%(#%#((##(",",9/8B#/9&,?#&<#&9#&#.9.#.##.",",;26?#23=++=+02.0#2#=+#00##0","-+#F#>+#6+#.+#&+(#&%#&#$%$#$##$","-928?#2.<./2-0#2/1$/0$#<.#0/##0",",3->D#-:#-#83+0+0-&0#-#0+##0",",;66;#6#1;-#1#'-)#'%#'#%%##%",",:67;#6:5$:4$:3$#3:+#3#++##+",",968;#6:5$95$#59)#5#/)#))##)",
",1/@B#/6#/#>1#010/$0))0#)##0",",9889#8#79-+/1#+-''-#'#--##-","","","4L#&I#&F#&C#&@#&=#&:#&7#&4#&1#&.#&+#&(#&%#&#$%$#$##$",".K#'G#'C#'?#';#'7#'3#'/#'+#''#'##'","0J#(E#(@#(;#(6#(1#(,#('#(#$'&#$%#$$#$##$","-I#)C#)=#)7#)1#)+#)%#)#'%#%%##%",".H#*A#*:#*3#*,#*%#*#(%#&%#$%$#$##$","*G#+?#+7#+/#+'#+#''##'",".F#,=#,4#,+#,&'('#'#)&$'%#($#'$##'","+E#-;#-1#-'#-#)'#%'%#%##%","'D#.9#..#.##.",")C#/7#/+#/#'+'#'##'",",B#05#0(#0#+(#&(%#&#$%$#$##$",",A#13#1+)+-#)+'%#)+)'%)#'##)",",@#28*+9#*2,)6*%4*%2*%2#*##2",")?#3/#3#'/+#''#'##'",",>#4-#4#*-&#*#'&#$&%#$$#$##$","+=#5+#5#-+#%+)#%'#%%#%##%",",<#6)#6#0)#*)%&'&#&#(%#&%##&",");#7/+/3#+#+/+#+##+",",:#8,*13#*,#*#/,#&,)#&&#&##&","%9#9##9",",8#:*,1/#,,)&,&&,#*#,*##,",")7#;+//+#/#3+#++##+",",6#<#)60#)*#)&%'(#%&#%#&&##&","+5#=#+5-#+%#+#)%#'%#%%##%",",4#>#-4*#-#&*'#&$#&#%$#$$##$",")3#?#/3'#/#+'#''##'",
",2#@,:)/7&,7&-2(#7,(2(#2(##2","+;-7E#-;#-#);5#)/#))#)##)",",0#B#50#(0+#(&#(#%&$#%#$$##$",")/#C#7/#+/'#+#''##'","'.#D#9.#..##.","+-#E#;-#1-#'-)#'%#'#%%##%",",;27@#21<-12-1#2#81#*1*#*##*","*+#G#?+#7+#/+#'+'#'##'",",:38?#3=1%;1%:2$:1$#1:1#1##1","+939?#3;/'#397/'3/'3#/##3",",50=B#05#0#85),/,#,#2)#,)##,",");77;#7#3;+#3#++##+",",85:=#580(#7810**0*0#0#0*##0","+979;#7#79/+/3#+#+/+#+##+",",54=>#4#<5-4+-#4#2-#(-(#(##(","","","2M#&J#&G#&D#&A#&>#&;#&8#&5#&2#&/#&,#&)#&&#&##&","2L#'H#'D#'@#'<#'8#'4#'0#',#'(#'$#'#&$#%$#$$##$",",K#(F#(A#(<#(7#(2#(-#((#(##(",",J#)D#)>#)8#)2#),#)&#)#&&##&",".I#*B#*;#*4#*-#*&#*#'&#$&%#$$#$##$","-H#+@#+8#+0#+(#+#&(%#&#$%$#$##$","(G#,>#,5#,,#,##,",")F#-<#-2#-(#-#((##(","-E#.:#./#.'&+,#&)#&#*'#&'&#&##&","*D#/8#/,#/#&,)#&&#&##&",",C#06#0)#0#*)%&'&#&#(%#&%##&",",B#14#1*'-0#',#'*%%*#%#**##*","&A#22#2##2",
"-@#30#3#&0-#&*#&'#&$#&#%$#$$##$",",?#4.#4#).(#)%&&%#&#'%#%%##%","'>#5,#5#,,##,",",=#6*#6#/*#(*%#(#&%#$%$#$##$",")<#7(#7#2(#-(#((##(","+;#8/,/2#,/)&#,/,)&,#)##,",",:#9/../#.#-/)')+#'#')'#'##'",",9#:-./.#.'4)'.)#6'#2'#.'##.","+8#;,//,#/#2,#),&#)#&&##&",")7#<#(72#(-#((#(##(",",6#=#*6/#*(#*#%(&#%$#%#$$##$","'5#>#,5,#,##,",",4#?#.4)#.#()&%&'#%#%&%#%##%","-3#@#03�#-&#*&#'&#$&%#$$#$##$","&2#A#22##2",",1#B#41'*-*#*#0'#,'%*%#*%##*",",0#C#60#)0*#)&%'(#%&#%#&&##&","*/#D#8/#,/&#,#)&#&&##&",",?44?#4+171#1#=+#5+'1'#1'##1",")-#F#<-#2-#(-(#(##(","(,#G#>,#5,#,,##,",",=56D)/J#)D#)=.*#.=9#..#.##.",",=66=#6#/=1#/)'+-#')#'#))##)","+2,AG#,>#,5#,#;2#,2,#,##,","*<77<#7#2<-#2#(-(#(##(","-40?C#06#0#;4)0.)#0#5)#/)#))##)","*;88;#8#5;)#5#/)#))##)",",97:D+/H#+#8987$8+/@#+8#+##8","-/.DE#.:#./#.#C/#7/#+/'#+#''##'","",
"","5N#&K#&H#&E#&B#&?#&<#&9#&6#&3#&0#&-#&*#&'#&$#&#%$#$$##$","0M#'I#'E#'A#'=#'9#'5#'1#'-#')#'%#'#%%##%","0L#(G#(B#(=#(8#(3#(.#()#(&%&'#%#%&%#%##%","-K#)E#)?#)9#)3#)-#)'#)#%'%#%##%",".J#*C#*<#*5#*.#*'#*#&'$#&#%$#$$##$",",I#+A#+9#+1#+)#+#%)'#%%#%##%","-H#,?#,6#,-#,('()#'#'(%#'#%%##%","+G#-=#-3#-)#-#')%#'#%%##%",",F#.;#.0#.)'*,#'#()('$(#'##(","+E#/9#/-#/'))'#)#+'#''##'",",D#07#0*#0#)*&%'(#%&#%#&&##&","+C#15#1'#1#-'#)'#%'%#%##%",",B#28(-=#(8#()#2#,)#&)&#&##&",",A#31#3)++)#+#-)#')%#'#%%##%",",@#4/#4#(/*#(%#(#&%#$%$#$##$","+?#5-#5#+-%#+#)%#'%#%%##%",",>#6+#6#.+#&+(#&%#&#$%$#$##$","+=#7)#7#1)#+)#%)'#%%#%##%",",<#80,/3#,2+$1+$0+$#+0+#+##+","+;#9+)35#)/#)#1+#)+)#)##)","%:#:##:","+9#;)+31#+)#+#5)#/)#))##)",",8#<,0/2*),*)1#*#3,#*,*#*##*","+7#=#)71#)+#)%#)#'%#%%##%",",6#>#+6.#+&#+#(&#%&$#%#$$##$","+5#?#-5+#-#%+)#%'#%%#%##%",",4#@#/4(#/#*(#%(&#%$#%#$$##$","+?/5E#/-/59#/-#/#7-#--##-",",2#B,<)-7(-2(&<)#?&#<-##2",
"+1#C#51#'1-#')#'%#'#%%##%",",0#D#70#*0)#*%&'&#&#(%#&%##&","+/#E#9/#-/)')+#'#')'#'##'",",.#F#;.#0.')*(#)'($#,'#('##(","+-#G#=-#3-#)-'#)#%'%#%##%",",=47@#40;064*#;0/4*/#4#//##/",",+#I#A+#9+#1+#)+%#)#'%#%%##%",",<58?#5<2&>1$=1$<1$#1<1#1##1","+3-AG#-=#-3#-#;3#+3+#+##+",",;69>#6;3&;0&;-4-*4#-##4","+51?C#15#1#;5#)5/#))#)##)",",52?B#2#<5,3,42$32$3#2#3,##3","+;99;#9#7;/+/3#+#+/+#+##+",",43@A#39++9#+4.(#?4#.4.#.##.","","","5O#&L#&I#&F#&C#&@#&=#&:#&7#&4#&1#&.#&+#&(#&%#&#$%$#$##$","2N#'J#'F#'B#'>#':#'6#'2#'.#'*#'&#'#$&%#$$#$##$","0M#(H#(C#(>#(9#(4#(/#(*#(%#(#&%#$%$#$##$","/L#)F#)@#):#)4#).#)(#)%&&%#&#'%#%%##%",".K#*D#*=#*6#*/#*(#*#%(&#%$#%#$$##$","/J#+B#+:#+2#+*#+&''&#'#(&#%&$#%#$$##$",".I#,@#,7#,.#,%#,#*%#(%#&%#$%$#$##$","-H#->#-4#-*#-#&*'#&$#&#%$#$$##$","-G#.<#.1#.&#.#+&#(&#%&$#%#$$##$","-F#/:#/.#/&'+*#'&#'#,&#)&#&&##&",",E#08#0+#0#(+&#(#%&$#%#$$##$",",D#16#1.)+0#)*-'*)'*#)#**##*","-C#24#2(&/1#&.#&+#&(#&#-(#((##(",",B#38)-<#)9&&9#&3.(3)(3#)##3",
"-A#40#4#'0,#'(#'$#'#&$#%$#$$##$",",@#5.#5#*.'#*#&'$#&#%$#$$##$",",?#6,#6#-,'(('#(#)'#%'%#%##%",",>#7*#7#0*#)*&%'(#%&#%#&&##&",",=#81,/4#,1)&1&&1#&#*1*#*##*",",<#91..1#.#+1)#+#%)'#%%#%##%",",;#:,+23#+#1,&+)+#+#.&#+&##+",",:#;+,21#,+&).#&+#+#++##+",",9#<.1.1)+3#)1'%1%%1#%#1.##1",",8#=,1/1**1#*#4,)1&&1&##1",",7#>#*70#*)#*%&'&#&#(%#&%##&",",6#?#,6-#,('()#'#'(%#'#%%##%",",5#@#.5*#.#'*&#'#$&%#$$#$##$",",C22C#2/-79#-/#-#5/#)/)#)##)",",3#B)8-.3()3(#<)#6)&3&##3","-2#C#42&(/-#((#(#1&#.&#+&#(&##(",",1#D#61).+-*')*'*#*#0)#*)##*",",0#E#80#+0(#+#&(%#&#$%$#$##$",",@45A#4.450#4.2%.0%#;.#0.##0",",?46A#4?2%*282#2#@*#9*#2*##2",",?56@#51:1:5(:/):)):#)#:1##:",",?66?#6/9371+/1+1#1#=/#1/##1",",=58I,,I#,=)/C#)=#)#0=0#0##0",",=68?#6=4%=2%>1$=1$#1=1#1##1",",<69?#6<3</#3#'/+#''#'##'",",=88=#8#3=-#3#)-'#)#%'%#%##%",".;7:>#7<5%<3%;6$#6;93&63&6++6#+##6",",52@C#2#=5,4,43$42$4#2#4,##4",",64?A#4#=607)34&04&0#4#00##0",",98<=#894'90'#;9.0.0#0#0.##0",
"","","3P#&M#&J#&G#&D#&A#&>#&;#&8#&5#&2#&/#&,#&)#&&#&##&","/O#'K#'G#'C#'?#';#'7#'3#'/#'+#''#'##'","0N#(I#(D#(?#(:#(5#(0#(+#(&#(#%&$#%#$$##$","+M#)G#)A#);#)5#)/#))#)##)",".L#*E#*>#*7#*0#*)#*%&'&#&#(%#&%##&",")K#+C#+;#+3#++#+##+","+J#,A#,8#,/#,&#,#)&#&&##&",",I#-?#-5#-+#-#%+)#%'#%%#%##%","-H#.=#.2#.'#.#*'#&'$#&#%$#$$##$","'G#/;#//#/##/","-F#09#0,#0#',(#'$#'#&$#%$#$$##$","+E#17#1)#1#+)#%)'#%%#%##%","*D#25#2,),/#)#),)#)##)","&C#33#3##3",",B#41#4'*-*#*#0'#,'%*%#*%##*","(A#5/#5#)/)#)##)",",@#6-#6#,-('()#'#'(%#'#%%##%",")?#7+#7#/+#'+'#'##'","*>#8)#8#2)#,)#&)&#&##&","*=#91-/3#-1+%#+1+#+##+",",<#:+)46#)0#)#2+#*+*)$*#)##*","%;#;##;",",:#<)+42#+*#+)*$#6)#0)#*)##*","*9#=-1/#3-+1%+#1#++##+","*8#>#)82#),#)&#)#&&##&",")7#?#+7/#+'#+#''##'",",6#@#-6,#-'(('#(#)'#%'%#%##%","(5#A#/5)#/#))##)",
",4#B#14*'-0#',#'*%%*#%#**##*","&3#C#33##3","*2#D#52),,)#,#/)#))##)","+1#E#71#)1+#)%#)#'%#%%##%","-0#F#90#,0'#,#('#$'&#$%#$$#$##$","'/#G#;/#//##/","-.#H#=.#2.#'.*#'&#'#$&%#$$#$##$",",-#I#?-#5-#+-%#+#)%#'%#%%##%","+,#J#A,#8,#/,#&,)#&&#&##&","(;3;C#3#3;3#3##3",",70?F#09#07.%#87-.-.#.#.-##.","*;5;A#5;/)#5;5/)5#/##5",",=89E*1L#*E#*A4'=4'#4=4#4##4","*3/CG#/;#/#?3#/3/#/##/","*52AD#25#2#>5#,5,#,##,","+53AC#3#?5)3/3#3#9)#3)##3","-76?@#69/*74%#>7-4-4/(4#/#4-##4","","","6Q#&N#&K#&H#&E#&B#&?#&<#&9#&6#&3#&0#&-#&*#&'#&$#&#%$#$$##$","3P#'L#'H#'D#'@#'<#'8#'4#'0#',#'(#'$#'#&$#%$#$$##$","1O#(J#(E#(@#(;#(6#(1#(,#('#(#$'&#$%#$$#$##$","/N#)H#)B#)<#)6#)0#)*#)&%'(#%&#%#&&##&","*M#*F#*?#*8#*1#**#*##*","/L#+D#+<#+4#+,#+'&()#&'$%(#$'#$#''##'",".K#,B#,9#,0#,'#,#('#$'&#$%#$$#$##$","-J#-@#-6#-,#-'(('#(#)'#%'%#%##%","-I#.>#.3#.(#.#)(%&&%#&#'%#%%##%","-H#/<#/0#/'&,-#&*#&'#&#+'#''##'","-G#0:#0-#0#&-*#&'#&$#&#%$#$$##$",
"(F#18#1*#1#**##*",",E#26#2,(-1#(,#(#),&#)#&&##&","-D#3:)->#)3,*7)&8#)7($3('3#(##3","-C#42#4&(/-#((#(#1&#.&#+&#(&##(",",B#50#5#(0+#(&#(#%&$#%#$$##$",",A#6.#6#+.&#+#(&#%&$#%#$$##$","-@#7,#7#.,#%,*#%(#%&#%$#%#$$##$","(?#8*#8#1*#**##*",",>#93..3#.#)3-#)'#)#%'%#%##%",",=#:0-03#-1+%1)%#-0-)'-#)##-",",<#;,+34#+,#+#2,#),&#)#&&##&",",;#<+,32#,,&)/#&,#+#,+##,",",:#=-00-#0#3-#)-'#)#%'%#%##%",",9#>.3.3-)3')5#'3%%3#%#3.##3","(8#?#*81#**#*##*","-7#@#,7.#,%#,#*%#(%#&%#$%$#$##$",",6#A#.6+#.#&+(#&%#&#$%$#$##$",",5#B#05(#0#+(#&(%#&#$%$#$##$","-4#C#24(&/1#&.#&+#&(#&#-(#((##(","-3#D,=*(@')=&)3-(?$#?(#9)#3)##3",",2#E#62(,-)#,#1(#,(#&)&#&##&","(1#F#81#*1*#*##*",",A46C#4B3$A3$-373#3#=-#3-##3",",A56B#5292=5'95'9,,9#,#92##9",",A66A#6-57/#5#?-#5-#)/)#)##)",",>49C#4>/(?+'#/>;+';#+/#/##/",",<3;D#3<++<#+#2<-#2#(-(#(##(",",<4;C#40@/04/2#402%#?0#20##2","(?88?#8#1?1#1##1","-2,EK#,B#,9#,#?2#020.%0,%0#,##0",
"-3.DI#.>#.3#.#?3#/3'#/#+'#''##'",",=9:0C0#C039->#93..#333#.##3",",74@C#4#=7.4,2#402%.2%#2.##2",",53BD#3#@5)4/43$4#3#:)#4)##4",",65AB#5#@6+5.0#5+0(#8+#0+##0","","","6R#&O#&L#&I#&F#&C#&@#&=#&:#&7#&4#&1#&.#&+#&(#&%#&#$%$#$##$","1Q#'M#'I#'E#'A#'=#'9#'5#'1#'-#')#'%#'#%%##%","-P#(K#(F#(A#(<#(7#(2#(-#((#(##(",".O#)I#)C#)=#)7#)1#)+#)%#)#'%#%%##%","0N#*G#*@#*9#*2#*+#*'&'(#&'%$#&'&%$&#%##&","-M#+E#+=#+5#+-#+%#+#)%#'%#%%##%",".L#,C#,:#,1#,(#,#'($#'#&$#%$#$$##$","(K#-A#-7#--#-##-","-J#.?#.4#.)#.#()&%&'#%#%&%#%##%","+I#/=#/1#/)'+-#')#'#))##)",",H#0;#0.#0')*(#)'($#,'#('##(","+G#19#1+#1#)+%#)#'%#%%##%",")F#27#2(#2#-(#((##(",",E#35#3+)-/#)+%'-#%+#%#++##+","-D#4:*-=#*:'&4.)4()9'$9#'4#(##4","+C#51#5#'1-#')#'%#'#%%##%",",B#6/#6#*/(#*#%(&#%$#%#$$##$","'A#7-#7#--##-",",@#8+#8#0+#(+&#(#%&$#%#$$##$","+?#9)#9#3)#-)#')%#'#%%##%",",>#:3/.8))8#)3*(#*31#**#*##*","+=#;+)57#)1#)+#)#3+#++##+","%<#<##<",
"+;#=)+53#++#+#7)#1)#+)##+",",:#>/3.2++2#+12$02$/2$#2/##2","+9#?#)93#)-#)'#)#%'%#%##%",",8#@#+80#+(#+#&(%#&#$%$#$##$","'7#A#-7-#-##-",",6#B#/6*#/#(*%#(#&%#$%$#$##$","+5#C#15'#1#-'#)'#%'%#%##%",",C25F#2C/&./8:#/.#/#9.#..##.",",3#E#53)+-+#+#/)%+'#-%#+%##+",")2#F#72#(2-#((#(##(","+1#G#91#+1)#+#%)'#%%#%##%",",0#H#;0#.0)'*,#'#()('$(#'##(","+/#I#=/#1/')+)#)#-'#)'##)",",=2;F#2=),@#)=&&=#�=0#0##0","(-#K#A-#7-#--##-",",?69B#64A.46.#;4/6(/#6#//##/","+=5;C#5A3%?3%=3%#3=3#3##3",",=6;B#6=1(#4=:1&71&41&4#1##4","+?99?#9#3?/#3#'/+#''#'##'",")<7<A#7#7<-#7#--##-","+3/EI#/=#/#A3#131/%1#/##1",",41DG#19#14,(#A4#040,'0#,##0","+53CE#35#3#A5#/5)#/#))##)","-<;<#;<=#;+)57#)1#)+#)#3+#++##+","","","4S#&P#&M#&J#&G#&D#&A#&>#&;#&8#&5#&2#&/#&,#&)#&&#&##&","3R#'N#'J#'F#'B#'>#':#'6#'2#'.#'*#'&#'#$&%#$$#$##$","1Q#(L#(G#(B#(=#(8#(3#(.#()#(&%&'#%#%&%#%##%","-P#)J#)D#)>#)8#)2#),#)&#)#&&##&",
"/O#*H#*A#*:#*3#*,#*%#*#(%#&%#$%$#$##$",".N#+F#+>#+6#+.#+&#+#(&#%&$#%#$$##$","+M#,D#,;#,2#,)#,#&)&#&##&","-L#-B#-8#-.#-(')*#'(%%(#%#((##(","-K#.@#.5#.*#.#'*&#'#$&%#$$#$##$","+J#/>#/2#/&#/#,&#)&#&&##&","-I#0<#0/#0&',+#''#'#-&#*&#'&##'","-H#1:#1,#1#(,'#(#$'&#$%#$$#$##$","*G#28#2)#2#,)#&)&#&##&",",F#36#3,)-0#)#*,+)$*)$*#)##*","&E#44#4##4","*D#52#5),,)#,#/)#))##)",",C#60#6#)0*#)&%'(#%&#%#&&##&","-B#7.#7#,.%#,#*%#(%#&%#$%$#$##$","*A#8,#8#/,#&,)#&&#&##&","-@#95..5#.#'51#'-#')#'%#'#%%##%","-?#:(#:#5(#0(#+(#&(%#&#$%$#$##$","+>#;2//2#/#,2)#,#&)&#&##&",",=#<0/01#/#/0)'+-#')#'#))##)",",<#=01/4)+6#)0-'0)'0#)#00##0","+;#>/2/2),5#)2&&2#/##2","-:#?#(:5#(0#(+#(&#(#%&$#%#$$##$","-9#@.5.51'5-'5)'5%'7#%5#%#5.##5","*8#A#,8/#,&#,#)&#&&##&","-7#B#.7,#.#%,*#%(#%&#%$#%#$$##$",",6#C#06)#0#*)%&'&#&#(%#&%##&","*5#D#25,),/#)#),)#)##)","&4#E#44##4",",3#F#63),-*#,)+$)*$#0)#*)##*","*2#G#82#)2,#)&#)#&&##&",
"-1#H#:1#,1(#,#'($#'#&$#%$#$$##$",",C66C#6/571#5/3%/1%#=/#1/##1","+/#J#>/#2/#&/,#&)#&&#&##&","-.#K#@.#5.#*.'#*#&'$#&#%$#$$##$","--#L#B-#8-#.-'()(#(#*'%(%#(%##(","*A88A#8#/A5#/)#/#))##)",",>6;C#6@3&>4%?3$>3$#3>3#3##3","->7;B#7.?367+.7+.#7#D.#9.#..##.","+>8;A#8>5>/#5#)/)#)##)","-?::?#:#5?-#5#+-%#+#)%#'%#%%##%",",<8=#9<A#8<3(96&93&9++9#+##9","+85AD#5#>8/5,2#5/2/##2","-42EG#28#25/&#C4#242/&2))2#)##2",",;:>?#:;6';2'#=;02.0#2#00##0","","","7T#&Q#&N#&K#&H#&E#&B#&?#&<#&9#&6#&3#&0#&-#&*#&'#&$#&#%$#$$##$","0S#'O#'K#'G#'C#'?#';#'7#'3#'/#'+#''#'##'","1R#(M#(H#(C#(>#(9#(4#(/#(*#(%#(#&%#$%$#$##$",".Q#)K#)E#)?#)9#)3#)-#)'#)#%'%#%##%","/P#*I#*B#*;#*4#*-#*&#*#'&#$&%#$$#$##$","+O#+G#+?#+7#+/#+'#+#''##'",".N#,E#,<#,3#,*#,#%*(#%&#%$#%#$$##$",",M#-C#-9#-/#-)')+#'#')'#'##'","-L#.A#.6#.+#.#&+(#&%#&#$%$#$##$","*K#/?#/3#/'#/#+'#''##'","'J#0=#00#0##0","+I#1;#1-#1#'-)#'%#'#%%##%","-H#29#2-&/6#&3#&0#&-#&#(-(#(##(","*G#37#3'#3#/'#+'#''##'",
"-F#4D2%D0%D.%D,%<,+=#,4,+4#,##4",",E#53#5)+-+#+#/)%+'#-%#+%##+",",D#61#6).+-*')*'*#*#0)#*)##*",")C#7/#7#+/'#+#''##'",",B#8-#8#.-'()(#(#*'%(%#(%##(","+A#9+#9#1+#)+%#)#'%#%%##%","-@#:)#:#4)#.)#()&%&'#%#%&%#%##%",")?#;3//3#/#+3+#+##+",".>#<1/08))8#)1(*3#(#.1.+&.(&.#(##.","%=#=##=",".<#>.01/#0#3.+0&(0&()*)#)#.(#)(##)",");#?/3/3++3#+#3/##3","-:#@#):4#).#)(#)%&&%#&#'%#%%##%","+9#A#+91#+)#+#%)'#%%#%##%",",8#B#-8.#-(')*#'(%%(#%#((##(",")7#C#/7+#/#'+'#'##'",",6#D#16.)+0#)*-'*)'*#)#**##*",",5#E#35+)-/#)+%'-#%+#%#++##+","-4#F2D%0D%.D%,D%,<+,4+#=,#4,##4","*3#G#73#'3/#'+#''#'##'",",D56E#51563#513%#:1*3*#3*##3","+1#I#;1#-1'#-#)'#%'%#%##%","'0#J#=0#00##0","*/#K#?/#3/#'/+#''#'##'",",?4;F#41>154-5#4#>1#,5,#,##,","+?5;E#5?/)?))?#)#1?1#1##1","-6-DM#-C#-9#-#;6/4*/-*/#-#//##/",")?7;C#7?3'#3?3#3##3","->7<C#7>2(>-(>((>#(#5>,#5#,,##,","+=7=C#7?3'?/'#7=7/+7#/##7",
",<7>C#7#9<:7%98$97$9--9#-##9","*3/GK#/?#/3#/#C3#33##3",".<9>A#9<4(#;<54*.4*0#4.2%.0%#0.##0","+=;=?#;#;=/+37#+/#+#//##/","-54EF#45#4#D5#25,),/#)#),)#)##)","","","7U#&R#&O#&L#&I#&F#&C#&@#&=#&:#&7#&4#&1#&.#&+#&(#&%#&#$%$#$##$","4T#'P#'L#'H#'D#'@#'<#'8#'4#'0#',#'(#'$#'#&$#%$#$$##$","1S#(N#(I#(D#(?#(:#(5#(0#(+#(&#(#%&$#%#$$##$","0R#)L#)F#)@#):#)4#).#)(#)%&&%#&#'%#%%##%","/Q#*J#*C#*<#*5#*.#*'#*#&'$#&#%$#$$##$",".P#+H#+@#+8#+0#+(#+#&(%#&#$%$#$##$","/O#,F#,=#,4#,+#,&'('#'#)&$'%#($#'$##'",".N#-D#-:#-0#-&#-#*&#'&#$&%#$$#$##$",".M#.B#.7#.,#.#%,*#%(#%&#%$#%#$$##$","-L#/@#/4#/(#/#*(#%(&#%$#%#$$##$","-K#0D)*E#)=)*?#)='%=%%=#%0#0##0","-J#1<#1.#1#&.+#&(#&%#&#$%$#$##$","-I#2:#21),4#)(),.#)(#)#-(#((##(","-H#38#3(#3#.(#)(%&&%#&#'%#%%##%",".G#46#4*(/1#(,#(*&%#-*#&*)#&&#&##&","-F#5=,,=#,+#5#-+#%+)#%'#%%#%##%",",E#62#6(,-)#,#1(#,(#&)&#&##&",",D#70#7#*0)#*%&'&#&#(%#&%##&",",C#8.#8#-.(')*#'(%%(#%#((##(",",B#97..7#.+-/-#-#1+'-'#-'##-","-A#:*#:#3*#,*#%*(#%&#%$#%#$$##$",".@#;(#;#6(#1(#,(#'($#'#&$#%$#$$##$",".?#<30/7(+:#(3,'5*%5(%5#(#,3,#,##,",
",>#=1001#0#/1)'+-#')#'#))##)",",=#>/010#0'6+)0)#:'#6'#0)##0",".<#?03/2)-6#)2%'4#%2#%12$02$#20##2",".;#@#(;6#(1#(,#('#(#$'&#$%#$$#$##$",",I22I#25-7?#-5#-#/5)#/#))##)",",9#B.7./--/#-#7.#+/'#+#''##'",",8#C#.8-#.'()(#(#*'%(%#(%##(",",7#D#07*#0#)*&%'(#%&#%#&&##&",",6#E#26,(-1#(,#(#),&#)#&&##&","-5#F,=,-5+#=,%5+#;%#9%#7%#5%##5",".4#G#64(*/-#*#1(#,(&*%&#*#)&#&&##&","-3#H#83#(3.#()#(&%&'#%#%&%#%##%","-2#I#:2)1,)(,-#(#4)#.)#()(#(##(",",D67E#6D5$D4$.494#4#?.#4.##4","-0#K.I%,I%*I%*C)*=)#D*#=*#00##0",",A5:F#52=2=9'=5'=,,=#,#=2##=","-C88C#8#-C9#-/#-)')+#'#')'#'##'",".-#N#D-#:-#0-#&-*#&'#&$#&#%$#$$##$","-7.DM#.B#.7#.#;7+//+#/#3+#++##+",",@8;C#8@5&A3%@4$@3$#3@3#3##3","-A::A#:/?5/-57#-#E/#9/#-/-#-##-","-60EK#0>#0:,'6,'#?6#,65#,,#,##,",",?:<A#:?8%@7$?7$#7?-#7#--##-",".84C#?8G#4/6,64%6#4&6,#<	&##6",",96BE#6#?906,2#604%02%#20##2",",=;>#<=H+3P#+H#+<;$<//<#/##<","-21IJ#1<#1#H2#92.5'.1'.#1#..##.","","","5V#&S#&P#&M#&J#&G#&D#&A#&>#&;#&8#&5#&2#&/#&,#&)#&&#&##&",
"2U#'Q#'M#'I#'E#'A#'=#'9#'5#'1#'-#')#'%#'#%%##%","2T#(O#(J#(E#(@#(;#(6#(1#(,#('#(#$'&#$%#$$#$##$",",S#)M#)G#)A#);#)5#)/#))#)##)","/R#*K#*D#*=#*6#*/#*(#*#%(&#%$#%#$$##$","-Q#+I#+A#+9#+1#+)#+#%)'#%%#%##%",")P#,G#,>#,5#,,#,##,",",O#-E#-;#-1#-'#-#)'#%'%#%##%","-N#.C#.8#.-#.'()(#(#*'%(%#(%##(",")M#/A#/5#/)#/#))##)",".L#0?#02#0(&-/#&,#&)#&#+(#&(&#&##&","+K#1=#1/#1')+)#)#-'#)'##)","*J#2;#2,#2#),&#)#&&##&","+I#39#3)#3#-)#')%#'#%%##%",",H#47#4,).1#)#+,+*$+)$+#)##+","&G#55#5##5",",F#63#6),-*#,)+$)*$#0)#*)##*","+E#71#7#)1+#)%#)#'%#%%##%","*D#8/#8#,/&#,#)&#&&##&","+C#9-#9#/-'))'#)#+'#''##'",",B#:7/.,/.6#/#1,*/%*#/#**##*",")A#;)#;#5)#/)#))##)",".@#<2.15#.2+&#-20+%.+%-,$-+$-#+##-","+?#=1/13#/#/1'#/#+'#''##'","%>#>##>","+=#?/11/#1#3/#'/+#''#'##'","-I03L#0903?#09*)#*98#*1#**#*##*",");#A#);5#)/#))#)##)",",:#B/7./,.1#,/*%#6/#*/*#*##*","+9#C#-9/#-)')+#'#')'#'##'","*8#D#/8,#/#&,)#&&#&##&",
"+7#E#17)#1#+)#%)'#%%#%##%",",6#F#36,)-0#)#*,+)$*)$*#)##*","&5#G#55##5",",4#H#74),.+#,*+$)+$#1)#+)##+","+3#I#93#)3-#)'#)#%'%#%##%","*2#J#;2#,2)#,#&)&#&##&","+1#K#=1#/1)'+-#')#'#))##)",",@3<I#3@*,B#*#/@;*(;#*/#/##/",")/#M#A/#5/#)/)#)##)",",A6;F#6A1(A,(#0A=,'=#,0#0##0","+C99C#9#/C7#/+#/#'+'#'##'","(>5>G#5#5>5#5##5","+A9;C#9A7%A5%A3%#3A3#3##3","->7>E#7?1)#7>91)75%73%71%7#1##7","*A;;A#;#5A/#5#)/)#)##)",",@;<M//M#/@.0B#.#7@7.,7#.##7","-?;=M//M#/?-1C#-#9?93)9-)9#-##9","+>;>A#;#;>)#;#5)#/)#))##)","+?==?#=#;?/+37#+/#+#//##/","->=>U9'#=>U5'U1'I1/=1/K#1=#1##=","","","8W#&T#&Q#&N#&K#&H#&E#&B#&?#&<#&9#&6#&3#&0#&-#&*#&'#&$#&#%$#$$##$","4V#'R#'N#'J#'F#'B#'>#':#'6#'2#'.#'*#'&#'#$&%#$$#$##$",".U#(P#(K#(F#(A#(<#(7#(2#(-#((#(##(","0T#)N#)H#)B#)<#)6#)0#)*#)&%'(#%&#%#&&##&","/S#*L#*E#*>#*7#*0#*)#*%&'&#&#(%#&%##&","0R#+J#+B#+:#+2#+*#+&''&#'#(&#%&$#%#$$##$",".Q#,H#,?#,6#,-#,('()#'#'(%#'#%%##%","*P#-F#-<#-2#-(#-#((##(",
"(O#.D#.9#..#.##.","-N#/B#/6#/*#/#(*%#(#&%#$%$#$##$",".M#0@#03#0�#-&#*&#'&#$&%#$$#$##$","-L#1E**E#*7#1)#1#+)#%)'#%%#%##%",")K#2<#2-#2#(-(#(##(","-J#3:#3*#3#,*#%*(#%&#%$#%#$$##$",".I#48#4'#4#0'#,'#('#$'&#$%#$$#$##$",",H#5=*.A#*5-+:*&:#*5((5#(##5",".G#64#6(*/-#*#1(#,(&*%&#*#)&#&&##&",")F#72#7#(2-#((#(##(",",E#80#8#+0(#+#&(%#&#$%$#$##$","'D#9.#9#..##.","-C#:,#:#1,#(,'#(#$'&#$%#$$#$##$",",B#;3,29#,3&)6#&3#&#+3+#+##+",")A#<2-27#-#-2-#-##-",",@#=3003#0#-3)#-#')%#'#%%##%",",?#>.-45#-#3.+0&+-&+#-#++##+",",>#?-.43#.0+&-+-#+-+#+##+",",=#@0303)-7#)3%'5#%3#%#30##3",")<#A-22-#2#7-#--##-",",;#B,323++3#+#9,&3)#6&##3","-:#C#,:1#,(#,#'($#'#&$#%$#$$##$","'9#D#.9.#.##.",",8#E#08+#0#(+&#(#%&$#%#$$##$",")7#F#27(#2#-(#((##(","-?,>Q#,H#,?#,#+?7#+/#+'#+#''##'",",5#H*=.#A*-5+*:&#:*(5(#5(##5",",G66G#61397#31-)#;1#-1-#-##-",",F67G#6F5$1585#5#<1*5*#5*##5",")2#K#<2#-2(#-#((##(",
",C5:H#53<3<5*<)/B#)<#)#<3##<","-D79F#7.792#7#B.#7.#(2-#((#(##(",",A5<H#5A.*#0A?.%=.%=#.0#0##0","(.#O#D.#9.#..##.","*-#P#F-#<-#2-#(-(#(##(",",?6>G#61C12604#624%#C1#42##4",",:2CK#2<#2:0%#;:/0./#0#//##/",",@9=D#9@5'@1'#6@;1(61(6#1##6",",@:=C#:@7@/#7#+/'#+#''##'",")A<<A#<#7A-#7#--##-","-84EI#48#4#A8#,8/#,&#,#)&#&&##&","-?<>A#<@;$?;$#;?)#;#5)#/)#))##)","-97D#B9F#7A2(<2(.7.72(7#2#7.##7","->=?L/1N#/>/1B#/>+'>''>#'#>>##>","","","8X#&U#&R#&O#&L#&I#&F#&C#&@#&=#&:#&7#&4#&1#&.#&+#&(#&%#&#$%$#$##$","1W#'S#'O#'K#'G#'C#'?#';#'7#'3#'/#'+#''#'##'","2V#(Q#(L#(G#(B#(=#(8#(3#(.#()#(&%&'#%#%&%#%##%","/U#)O#)I#)C#)=#)7#)1#)+#)%#)#'%#%%##%","+T#*M#*F#*?#*8#*1#**#*##*","*S#+K#+C#+;#+3#++#+##+","/R#,I#,@#,7#,.#,%#,#*%#(%#&%#$%$#$##$",",Q#-G#-=#-3#-)#-#')%#'#%%##%",".P#.E#.:#./#.'&+,#&)#&#*'#&'&#&##&","*O#/C#/7#/+#/#'+'#'##'",".N#0A#04#0'#0#,'#('#$'&#$%#$$#$##$","'M#1?#11#1##1","-L#2=#2.#2#'.*#'&#'#$&%#$$#$##$","(K#3;#3+#3#++##+",
"-J#49#4(#4#/(#*(#%(&#%$#%#$$##$","+I#57#5-+-/#+#+-'#+#''##'",",H#6@.+;1(=.&=#.61(6**6#*##6","*G#73#7#'3/#'+#''#'##'","(F#81#8#*1*#*##*","+E#9/#9#-/)')+#'#')'#'##'","-D#:-#:#0-#&-*#&'#&$#&#%$#$$##$","(C#;+#;#3+#++##+",",B#<4.17#.4+&#+4/#+'#+#''##'",",A#=-)7;#)5#)/#)#3-#)-)#)##)",",@#>2013#02/$#/2'#/#+'#''##'","%?#?##?",",>#@/120#1/0$#4/+0''0'#0'##0","+I/5O#/7/5C#/7#/#-7-#-##-",",<#B.41#7.+4&+#4#/+#'+'#'##'","(;#C#+;3#++#+##+","-:#D#-:0#-&#-#*&#'&#$&%#$$#$##$","+9#E#/9-#/'))'#)#+'#''##'","(8#F#18*#1#**##*","*7#G#37'#3#/'#+'#''##'",",6#H1C(1>(*A*.>&.6+#A*#6.##6","+5#I#75+--+#-#/+#'+'#'##'","-4#J#94#(4/#(*#(%#(#&%#$%$#$##$","(3#K#;3#+3+#+##+","-2#L#=2#.2'#.#*'#&'$#&#%$#$$##$","'1#M#?1#11##1",".0#N#A0#40#'0,#'(#'$#'#&$#%$#$$##$","*/#O#C/#7/#+/'#+#''##'","-C8;F#8+8;1#8#H+#@+#8+#*1*#*##*",",-#Q#G-#=-#3-#)-'#)#%'%#%##%",
",@7>G#72D13703#72C$#C2#33##3","(C;;C#;#3C3#3##3","*?8?F#8?1*#8?81*8#1##8","-A;=C#;A9%A7%#7A/#7#+/'#+#''##'","-83FK#3;#3#A8*31+#3#:*#3*#++##+","*?;?C#;#;?+#;#3+#++##+",",>;@C#;>6(#=>76*06*0#6#00##0","+97EG#7#C93=)37)3#7#33##3",",;:CD#:;1,#B;/6/61(6#1#6/##6","","","6Y#&V#&S#&P#&M#&J#&G#&D#&A#&>#&;#&8#&5#&2#&/#&,#&)#&&#&##&","5X#'T#'P#'L#'H#'D#'@#'<#'8#'4#'0#',#'(#'$#'#&$#%$#$$##$","2W#(R#(M#(H#(C#(>#(9#(4#(/#(*#(%#(#&%#$%$#$##$",".V#)P#)J#)D#)>#)8#)2#),#)&#)#&&##&","1U#*N#*G#*@#*9#*2#*+#*'&'(#&'%$#&'&%$&#%##&","0T#+L#+D#+<#+4#+,#+'&()#&'$%(#$'#$#''##'",",S#,J#,A#,8#,/#,&#,#)&#&&##&",".R#-H#->#-4#-*#-#&*'#&$#&#%$#$$##$","-Q#.F#.;#.0#.)'*,#'#()('$(#'##(","+P#/D#/8#/,#/#&,)#&&#&##&","-O#0B#05#0(#0#+(#&(%#&#$%$#$##$","-N#1G**G#*9#1+#1#)+%#)#'%#%%##%","+M#2>#2/#2#&/,#&)#&&#&##&","-L#3<#3,#3#*,%#*#(%#&%#$%$#$##$","-K#4:#4)#4#.)#()&%&'#%#%&%#%##%","*J#58#5,)/2#),#)#,,##,","&I#66#6##6",",H#74#7),.+#,*+$)+$#1)#+)##+","*G#82#8#)2,#)&#)#&&##&",
"-F#90#9#,0'#,#('#$'&#$%#$$#$##$","-E#:.#:#/.&'+*#'&#'#,&#)&#&&##&","*D#;,#;#2,#),&#)#&&##&","-C#<*#<#5*#.*#'*&#'#$&%#$$#$##$",",B#=3.27#.+5+,.*,#.#5+#,,##,","*A#>2/25#/#/2)#/#))##)","-@#?+*89#*2#*+#*#7+#/+#'+'#'##'","-?#@*+87#+/#++''+#'#9*#2*#+*##+","*>#A/22/#2#5/#)/)#)##)",",=#B.325++5#+.,*#7.#,.,#,##,","-<#C#*<5#*.#*'#*#&'$#&#%$#$$##$","*;#D#,;2#,)#,#&)&#&##&",",K44K#45/9?#/#3531%3/%3#/##3","-9#F#09,#0#',(#'$#'#&$#%$#$$##$","*8#G#28)#2#,)#&)&#&##&",",7#H#47,).1#)#+,+*$+)$+#)##+","&6#I#66##6","*5#J#85),/,#,#2)#,)##,","-4#K#:4#)4.#)(#)%&&%#&#'%#%%##%","-3#L#<3#,3*#,#%*(#%&#%$#%#$$##$","*G88G#8/5;5#5#A/#5/##5","-1#N,I(,D(,?(#E,&?)#B&#?##1",",A4>K#4F/(A/(#1A?/%?#/1#1##1","*A5>J#5A,,A#,#2A2#2##2",",B7=H#7B1)#2BA1$A**A#*2#2##2","-B8=G#8B3(C/'C+'C''C#'#3B3#3##3","*A8>G#8D5&A5A5#5##5","->6AI#6/E2/626#6#H/#</)6)#6)##6","-C<<C#<#5C1#5#'1-#')#'%#'#%%##%",",82GM#2>#28,)#A8#,85#,,#,##,",
",@;?D#;@7'#:@=7&:7&:--:#-##:","-?;@T3+T++T#+#<?>;$=;$<;$<#;##<","*;8DG#8#A;28,2#8#22##2","-><AC#<#?>;<&;4+04.2#402%#20##2","-:9EF#9:-/<#-#D:#-:2#-(#-#((##(","","","9Z#&W#&T#&Q#&N#&K#&H#&E#&B#&?#&<#&9#&6#&3#&0#&-#&*#&'#&$#&#%$#$$##$","3Y#'U#'Q#'M#'I#'E#'A#'=#'9#'5#'1#'-#')#'%#'#%%##%","2X#(S#(N#(I#(D#(?#(:#(5#(0#(+#(&#(#%&$#%#$$##$","/W#)Q#)K#)E#)?#)9#)3#)-#)'#)#%'%#%##%","0V#*O#*H#*A#*:#*3#*,#*%#*#(%#&%#$%$#$##$",".U#+M#+E#+=#+5#+-#+%#+#)%#'%#%%##%","/T#,K#,B#,9#,0#,'#,#('#$'&#$%#$$#$##$","-S#-I#-?#-5#-+#-#%+)#%'#%%#%##%",".R#.G#.<#.1#.&#.#+&#(&#%&$#%#$$##$",",Q#/E#/9#/-#/'))'#)#+'#''##'","-P#0C#06#0)#0#*)%&'&#&#(%#&%##&","-O#1A#13#1+)+-#)+'%#)+)'%)#'##)","-N#2?#25(-:#(5#(,),/#)#),)#)##)","+M#3=#3-#3#)-'#)#%'%#%##%","-L#4;#4*#4#-*#&*'#&$#&#%$#$$##$",",K#59#5'#5#1'#-'#)'#%'%#%##%",".J#6;'2F#'B#'>#'61(6,(6'(:#'6#'##6","+I#75#7+--+#-#/+#'+'#'##'","-H#83#8#(3.#()#(&%&'#%#%&%#%##%","+G#91#9#+1)#+#%)'#%%#%##%","-F#:/#:#./'&+,#&)#&#*'#&'&#&##&","+E#;-#;#1-#'-)#'%#'#%%##%",".D#<+#<#4+#,+&'('#'#)&$'%#($#'$##'",
",C#=)#=#7)#1)#+)#%)'#%%#%##%",".B#>3/26#/4-%4+%3.$#.31+&.+&.#+##.","+A#?3113#1#/3'#/#+'#''##'","%@#@##@","+?#A/131#1#5/+1''1'#1'##1","-J/6Q#/7/6E#/9#/8.$7.$#.7.#.##.",",=#C#)=7#)1#)+#)%#)#'%#%%##%","-G.9R#.G#./,;>#,5#,#8/#,/,#,##,","+;#E#-;1#-'#-#)'#%'%#%##%","-:#F#/:.#/&'+*#'&#'#,&#)&#&&##&","+9#G#19+#1#)+%#)#'%#%%##%","-8#H#38(#3#.(#)(%&&%#&#'%#%%##%","+7#I#57-+-/#+#+-'#+#''##'",".6#J';216(,6('6(#F'#B'#>'#:'#6'##6",",5#K#95#'51#'-#')#'%#'#%%##%","-4#L#;4#*4-#*&#*#'&#$&%#$$#$##$","+3#M#=3#-3)#-#')%#'#%%##%","-2#N#?2(5-),,)#,#:(#5(#/)#))##)",",G99G#9#+G?#+7#+/#+'#+#''##'","-0#P#C0#60#)0*#)&%'(#%&#%#&&##&",",/#Q#E/#9/#-/)')+#'#')'#'##'","..#R#G.#<.#1.#&.+#&(#&%#&#$%$#$##$","--#S#I-#?-#5-#+-%#+#)%#'%#%%##%","-B9>G#9C5'B8$B7$B6$B5$#5B5#5##5","-A9?G#9A3)#7A=3'93'75%73%7#3##7","-C<=I(7X#(S#(N#(I#(C6)#6C6#6##6","+C==C#=#7C/#7#+/'#+#''##'","-@;@E#;A7'#;@=7';9%;7%;--;#-##;","+A=?C#=A;%#;A+#;#3+#++##+","-<9DG#9<..<#.#A<-22-#2#7-#--##-",
",31MO#1A#13#1#K3#;3#+3+#+##+","-65JK#5?)/E#)?#)6,,6#,#I6#66##6","","","9[#&X#&U#&R#&O#&L#&I#&F#&C#&@#&=#&:#&7#&4#&1#&.#&+#&(#&%#&#$%$#$##$","5Z#'V#'R#'N#'J#'F#'B#'>#':#'6#'2#'.#'*#'&#'#$&%#$$#$##$","3Y#(T#(O#(J#(E#(@#(;#(6#(1#(,#('#(#$'&#$%#$$#$##$","1X#)R#)L#)F#)@#):#)4#).#)(#)%&&%#&#'%#%%##%","0W#*P#*I#*B#*;#*4#*-#*&#*#'&#$&%#$$#$##$","/V#+N#+F#+>#+6#+.#+&#+#(&#%&$#%#$$##$","/U#,L#,C#,:#,1#,(#,#'($#'#&$#%$#$$##$",".T#-J#-@#-6#-,#-'(('#(#)'#%'%#%##%",".S#.H#.=#.2#.'#.#*'#&'$#&#%$#$$##$",".R#/F#/:#/.#/&'+*#'&#'#,&#)&#&&##&","-Q#0D#07#0*#0#)*&%'(#%&#%#&&##&","-P#1B#14#1*'-0#',#'*%%*#%#**##*","-O#2G*+H#*A,)E*%C*%A*%A#*2#2##2","-N#3>#3.#3#(.)#(&%&'#%#%&%#%##%",".M#4<#4+#4#,+&'('#'#)&$'%#($#'$##'","-L#5:#5(#5#0(#+(#&(%#&#$%$#$##$",",K#6A,-B#,A+$6+.:#+6''6#'##6","-J#7>+/B#+2+/:#+2#+#(2-#((#(##(",".I#84#8#'40#',#'(#'$#'#&$#%$#$$##$",",H#9=..=#./+15#+#-/-+%-#+##-","-G#:0#:#-0&#-#*&#'&#$&%#$$#$##$",",F#;.#;#0.')*(#)'($#,'#('##(",",E#<90/.1.80$8#01**1#*#1.##1",",D#=4-3:#-5((5#(4,$#,4,#,##,",",C#>4/27#/5-%4.$4-$#-4-#-##-",",B#?3025#04/$3/$#/3)#/#))##)",
"-A#@-,78#,/#,#6-#,-&#,#)&#&&##&","-@#A,-76#-,#-#8,#/,#&,)#&&#&##&",",?#B/230#2/1$/0$#6/)0)#0)##0",",>#C/42#7/-5%.4$-4$-#4#--##-",",=#D-43#:-(5(,4$,#4#5(#,,##,",",<#E09/1..1#.08$#80#*1*#*##*",",;#F#.;0#.)'*,#'#()('$(#'##(","-:#G#0:-#0#&-*#&'#&$#&#%$#$$##$",",9#H.=./3-1++1#+/1%#=.#1/##1","-G2:O#2>@,@9*@2*@#25@,,@,#@,##@",",I58L#5I2&=>/=2/=#2#0=0#0##0",",6#K2G'.G'.?+#@.-?$-6,#6-##6","-5#L#:5#(50#(+#(&#(#%&$#%#$$##$",",I88I#83795#735%#=3+5+#5+##5",",G7:J#7G4&G1&5<5<1.<#1#<5##<",",E6<K#6E0)4>4>7*>0*>#0#>4##>","-1#P#B1#41'*-*#*#0'#,'%*%#*%##*",",B5?L#5E.*B2BA.'A#.2#2##2",",B6?K#60@586-8#608+#E0#80##8","-C8>I#8C2)C,)C&)F#&C#C3#3##3","-E;<F#;,;<.#;,9%#K,#B,#9,#..##.",",C:>G#:C6'3E34624#6#E3#44##4",",A9@H#9B3)A8$#8A=3(83(8#3##8",",A:@G#:A4)D1&A1	A91+9#1##9",".?9BH#9B3)D/'#<?<9&<3)@/'</'<#/##<","-C>>C#>#9C-#9#/-'))'#)#+'#''##'",",?;BF#;?4*#>?54-5#4#,5,#,##,",",:7GJ#7#D:1;,67'6#716(#61##6","-86IK#68#6#G8#28)#2#,)#&)&#&##&","-@?AP11P#1@/3D#/@+'@''@#'#@@##@",
"","","7]#&Y#&V#&S#&P#&M#&J#&G#&D#&A#&>#&;#&8#&5#&2#&/#&,#&)#&&#&##&","2[#'W#'S#'O#'K#'G#'C#'?#';#'7#'3#'/#'+#''#'##'","/Z#(U#(P#(K#(F#(A#(<#(7#(2#(-#((#(##(","-Y#)S#)M#)G#)A#);#)5#)/#))#)##)","0X#*Q#*J#*C#*<#*5#*.#*'#*#&'$#&#%$#$$##$",",W#+O#+G#+?#+7#+/#+'#+#''##'",",V#,M#,D#,;#,2#,)#,#&)&#&##&",")U#-K#-A#-7#--#-##-",".T#.I#.>#.3#.(#.#)(%&&%#&#'%#%%##%","(S#/G#/;#//#/##/","-R#0E#08#0+#0#(+&#(#%&$#%#$$##$",",Q#1C#15#1'#1#-'#)'#%'%#%##%","'P#2A#22#2##2","*O#3?#3/#3#'/+#''#'##'",".N#4=#4,#4#+,'&()#&'$%(#$'#$#''##'",")M#5;#5)#5#/)#))##)","-L#69#6.+.1#+/)%#+.-)%+)%+#)##+","&K#77#7##7","*J#85#8),/,#,#2)#,)##,","+I#93#9#)3-#)'#)#%'%#%##%","-H#:1#:#,1(#,#'($#'#&$#%$#$$##$","'G#;/#;#//##/",")F#<-#<#2-#(-(#(##(",",E#=+#=#5+#-+#%+)#%'#%%#%##%","+D#>)#>#8)#2)#,)#&)&#&##&","+C#?3/37#/3+'#/3/+'/#+##/",",B#@/-68#-#4/).).-$.#-#.)##.","%A#A##A",
",@#B-/64#/.)).#)-.$#8-#.-##.","+?#C/33/#3#7/#+/'#+#''##'","+>#D#)>8#)2#),#)&#)#&&##&",",=#E#+=5#+-#+%#+#)%#'%#%%##%",")<#F#-<2#-(#-#((##(","';#G#/;/#/##/","-:#H#1:,#1#(,'#(#$'&#$%#$$#$##$","+9#I#39)#3#-)#')%#'#%%##%","*8#J#58,)/2#),#)#,,##,","&7#K#77##7",",H5:M#5>B-4B-;50;#54;*#;4##;",")5#M#;5#)5/#))#)##)",".4#N#=4#,4+#,&'('#'#)&$'%#($#'$##'","*3#O#?3#/3'#/#+'#''##'","'2#P#A2#22##2",",1#Q#C1#51#'1-#')#'%#'#%%##%","-0#R#E0#80#+0(#+#&(%#&#$%$#$##$","(/#S#G/#;/#//##/","-F;<G#;-;</#;#J-#@-(;(#;(#//##/","(A7AK#7#7A7#7##7","*D;>G#;D8&D5D5#5##5","+7/KS#/G#/;#/#C7#/7/#/##/",".D=>]:&]7&V7)P7)J7)K#7D7)#7D7#7##7",")A;AG#;#;A/#;#//##/","*72KP#2A#2#F7#272#2##2","*C??C#?#;C+#;#3+#++##+",",2/PS#/G#/;#/#M2#>2#/2/#/##/",",75KM#5;#5#I7#57)#5#/)#))##)","-87J#I8K#7,=/27)7#7,7)#@,#7,##7"
};
int T,n,m,id[61][61];
struct dat{
int x,y,L;
};
vector<dat>vec;
inline int decode(char c){return c-35-(c>=92);}
void get(int c){
vec.clear();
const char*s=A[c];
int sz=decode(*s);
for(int i=1;i<=sz;++i)vec.push_back((dat){decode(s[3*i-2]),decode(s[3*i-1]),decode(s[3*i])});
}
int main(){
freopen("hard.in","r",stdin);
freopen("hard.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
for(int i=1,c=0;i<=60;++i)
for(int j=1;j<i;++j)id[i][j]=c++;
for(cin>>T;T--;){
cin>>n>>m;
if(n==m)cout<<"1\n0 0 "<<n<<'\n';
else if(m==1){
cout<<n<<'\n';
for(int i=0;i<n;++i)cout<<i<<" 0 1\n";
}else if(n==1){
cout<<m<<'\n';
for(int i=0;i<m;++i)cout<<"0 "<<i<<" 1\n";
}else if(m==2){
cout<<n/2+n%2*2<<'\n';
for(int i=0;i<n/2;++i)cout<<2*i<<" 0 2\n";
if(n&1)cout<<n-1<<" 0 1\n"<<n-1<<" 1 1\n";
}else if(n==2){
cout<<m/2+m%2*2<<'\n';
for(int i=0;i<m/2;++i)cout<<"0 "<<2*i<<" 2\n";
if(m&1)cout<<"0 "<<m-1<<" 1\n1 "<<m-1<<" 1\n";
}else{
bool cur=0;
if(n<m)cur=1,swap(n,m);
get(id[n][m]);
if(cur)
for(int i=0;i<(int)vec.size();++i)swap(vec[i].x,vec[i].y);
cout<<vec.size()<<'\n';
for(dat i:vec)cout<<i.x<<' '<<i.y<<' '<<i.L<<'\n';
}
}
return 0;
}
BH
题目大意:
给定一个直角边长为 $w$ 和 $h$ 的直角三角形 $OAB$,令三个点的坐标分别为 $O(0,0)$,$A(w,0)$,$B(w,h)$。$\angle A$ 为直角。
你现在要添加 $n$ 条两个端点分别在 $OA$ 和 $OB$ 上,且垂直于 $OA$ 的线段 $l_1,l_2,\ldots,l_n$。
现在我们有 $AB$,$OB$ 以及 $l_1,l_2,\ldots,l_n$ 这 $n+2$ 条线段。对于这些线段上的任意一个点,它的代价是这个点经过这些线段到达 $OA$ 的距离。
要求找到一个添加线段的方案,使得总代价最小。输出最小价值,并按顺序输出添加的线段的横坐标(若 $n>10$ 则只输出前 $10$ 条线段的横坐标)。
$1\leq h\leq w\le 10^4$,$1\leq n\leq 10^3$。
题解:
一个重要的条件是 $h\leq w$。
我们对不同位置上的点分别考虑。
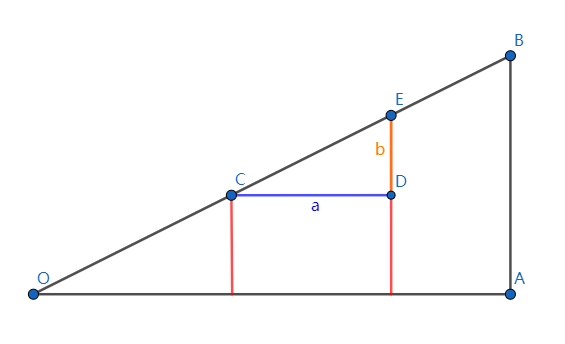
观察上图,易证 $\triangle OAB\sim \triangle CDE$,由 $h\leq w$ 可知 $b\leq a$。
对于在竖直线段上的点(以及它与 $OA$ 的交点),显然它从右边的竖直线段向上劣于从自己所在的竖直线段向上。考虑它从左边的竖直线段向上,则它至多减少 $b$ 的距离,至少增加 $a$ 的距离,由 $b\leq a$ 可知不优。因此从自己所在的竖直线段向上是最优的。
同理也可以证明,对于在水平线段上的点,它一定是选择它左边的第一条竖直线段(包括点 $O$)或右边的第一条竖直线段向上走。
由于竖直的线段垂直于 $OA$,故这条线段两个端点作为顶点,第三个顶点为 $O$ 的三角形和 $\triangle OAB$ 也相似。
考虑确定 $l_n$ 的位置,令 $l_n$与 $AB$ 的距离为 $L$。假设我们已经知道了 $l_n$ 的位置,那么我们只需要计算 $OA$ 最右边那段(长度为 $L$)以及 $AB$ 段的代价,剩下的就转化为添加 $n-1$ 条线段的子问题。
由于这个子问题对应的三角形和原问题的三角形相似,因此它对应的最优解,相当于原三角形添加 $n-1$ 条线段的最优解按比例缩放后的结果,所以我们考虑求出在原三角形上添加 $n-1$ 条线段的子问题。
假设已经知道了添加 $k-1$ 条线段的最优代价为 $C$,考察添加 $k$ 条线段时的最优代价 $C’$ 与 $L$ 的关系。我们只需要计算最右边的“L”形的代价即可。
我们考虑把它补成“U”形,它的长度为 $a$,则它的总代价为 $\frac{a^2}4$。然后减去左边那条重复计算的代价即可。
据此可列出式子。
可以发现,$C’$ 与 $L$ 是二次函数关系,直接求它的最小值即可。
最终每条线段的位置可以从后往前推得。
时间复杂度 $O(n)$。
Code:
#include<bits/stdc++.h>
using namespace std;
int w,h,n;
double C,x[1005];
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>w>>h>>n;
C=(w+h)*(w+h)/4.;
for(int i=1;i<=n;++i){
double a=(1-1.*h*h/w/w-2.*h/w)/4+C/w/w;
double b=h-2.*C/w;
double c=C+h*h/2.;
double L=-b/a/2;
x[i]=w-L,C=a*L*L+b*L+c;
}
cout<<fixed<<setprecision(8)<<C<<'\n';
double c=1;
for(int i=n;i;--i){
double d=c*x[i]/w;
x[i]*=c;
c=d;
}
for(int i=1;i<=n&&i<=10;++i)cout<<x[i]<<'\n';
return 0;
}
TH
题目大意:
给定一座山的地形信息(表面每个面均为三角形),以及表面的两个点 $A$ 和 $B$,要求找到一条从 $A$ 到 $B$ 的路线,只能在表面上走,并要求最大高度最小。输出方案。
令 $n$ 表示地形被划分成的三角形个数。
$1\leq n\leq 2000$,$0\leq x,y,z\leq 10^6$。
题解:
若一条路径从一个点走到一条边上,我们一定可以将在边上的那一端移动到这条边较低的点上,这并不影响它接下来能走到的地方,并且最大高度并不会变大。因此我们一定能找到一组最优方案,它只经过 $A$,$B$ 以及三角形的端点。
可以考虑二分最大高度,然后用 BFS 判定连通性。时间复杂度 $O(n\log V)$。
或者使用排序+并查集。时间复杂度 $O(n\log n)$ 或 $O(n\alpha(n)+V)$。
我们需要找到 $A$ 和 $B$ 所在的那个三角形。可以使用判断面积和是否相等的方法。求面积可以使用海伦公式暴算,误差约为 $10^{-2}$,将 eps 设为该值即可通过。
Code:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL _1=1e6+1,_2=_1*_1;
const int N=1e6+9;
unordered_map<LL,int>id;
int n,m,Xs,Ys,Zs,Xt,Yt,Zt,sz[N],fa[N],s,t;
LL ys[N];
inline LL _zip(int x,int y,int z){return x*_2+y*_1+z;}
struct dat{
int X1,Y1,Z1,X2,Y2,Z2,X3,Y3,Z3;
LL a1,a2,a3;
long double S;
}A[N];
vector<int>buc[N],G[N];
inline void addedge(int u,int v){G[u].emplace_back(v),G[v].emplace_back(u);}
inline long double length(int x,int y,int z){return sqrtl((LL)x*x+(LL)y*y+(LL)z*z);}
inline long double area(int X1,int Y1,int Z1,int X2,int Y2,int Z2,int X3,int Y3,int Z3){
long double p=length(X1-X2,Y1-Y2,Z1-Z2);
long double q=length(X1-X3,Y1-Y3,Z1-Z3);
long double r=length(X3-X2,Y3-Y2,Z3-Z2);
long double D=(p+q+r)/2;
return sqrtl(D*(D-p))*sqrt((D-q)*(D-r));
}
void work(){
for(int i=1;i<=n;++i){
long double S1=area(A[i].X1,A[i].Y1,A[i].Z1,A[i].X2,A[i].Y2,A[i].Z2,Xs,Ys,Zs)+
area(A[i].X3,A[i].Y3,A[i].Z3,A[i].X2,A[i].Y2,A[i].Z2,Xs,Ys,Zs)+
area(A[i].X1,A[i].Y1,A[i].Z1,A[i].X3,A[i].Y3,A[i].Z3,Xs,Ys,Zs);
if(fabsl(A[i].S-S1)<1e-2)addedge(s,A[i].a1),addedge(s,A[i].a2),addedge(s,A[i].a3);
S1=area(A[i].X1,A[i].Y1,A[i].Z1,A[i].X2,A[i].Y2,A[i].Z2,Xt,Yt,Zt)+
area(A[i].X3,A[i].Y3,A[i].Z3,A[i].X2,A[i].Y2,A[i].Z2,Xt,Yt,Zt)+
area(A[i].X1,A[i].Y1,A[i].Z1,A[i].X3,A[i].Y3,A[i].Z3,Xt,Yt,Zt);
if(fabsl(A[i].S-S1)<1e-2)addedge(t,A[i].a1),addedge(t,A[i].a2),addedge(t,A[i].a3);
}
}
bool vis[N];
inline int find(int x){while(x!=fa[x])x=fa[x]=fa[fa[x]];return x;}
inline void merge(int x,int y){
x=find(x),y=find(y);
if(x==y)return;
if(sz[x]<sz[y])swap(x,y);
fa[y]=x,sz[x]+=sz[y];
}
void final(){
static bool ur[N];
static int pre[N];
static queue<int>q;
ur[s]=1;
for(q.emplace(s);q.size();){
int u=q.front();q.pop();
for(int to:G[u])if(vis[to]&&!ur[to])ur[to]=1,pre[to]=u,q.emplace(to);
}
static vector<LL>ans;
for(int x=t;x;x=pre[x])ans.emplace_back(ys[x]);
reverse(ans.begin(),ans.end()),cout<<ans.size()<<'\n';
for(LL v:ans)cout<<v/_2<<' '<<v%_2/_1<<' '<<v%_1<<'\n';
}
void solve(){
for(int i=1;i<=m;++i)fa[i]=i,sz[i]=1;
for(int i=0;i<=1000000;++i){
for(int x:buc[i]){
vis[x]=1;
for(int to:G[x])if(vis[to])merge(x,to);
}
if(find(s)==find(t)){final();return;}
}
cerr<<"Unknown Error"<<'\n';
exit(1);
}
int main(){
freopen("hiking.in","r",stdin);
freopen("hiking.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;++i){
cin>>A[i].X1>>A[i].Y1>>A[i].Z1>>A[i].X2>>A[i].Y2>>A[i].Z2>>A[i].X3>>A[i].Y3>>A[i].Z3;
LL a1=_zip(A[i].X1,A[i].Y1,A[i].Z1),a2=_zip(A[i].X2,A[i].Y2,A[i].Z2),a3=_zip(A[i].X3,A[i].Y3,A[i].Z3);
if(!id.count(a1))buc[A[i].Z1].emplace_back(id[a1]=++m),ys[m]=a1;
if(!id.count(a2))buc[A[i].Z2].emplace_back(id[a2]=++m),ys[m]=a2;
if(!id.count(a3))buc[A[i].Z3].emplace_back(id[a3]=++m),ys[m]=a3;
addedge(id[a1],id[a2]),addedge(id[a1],id[a3]),addedge(id[a2],id[a3]);
A[i].a1=id[a1],A[i].a2=id[a2],A[i].a3=id[a3];
A[i].S=area(A[i].X1,A[i].Y1,A[i].Z1,A[i].X2,A[i].Y2,A[i].Z2,A[i].X3,A[i].Y3,A[i].Z3);
}
cin>>Xs>>Ys>>Zs>>Xt>>Yt>>Zt;
LL as=_zip(Xs,Ys,Zs),at=_zip(Xt,Yt,Zt);
if(!id.count(as))buc[Zs].emplace_back(id[as]=++m),ys[m]=as;
if(!id.count(at))buc[Zt].emplace_back(id[at]=++m),ys[m]=at;
s=id[as],t=id[at];
work();
solve();
return 0;
}
