【CQOI2017】老 C 的方块 | Mrsrz's blog

最小割。

题目大意：

给定 $C$ 行 $R$ 列的矩形，每个格子可能有方块或没方块。其中相邻两个格子之间有一条边。这条边有可能是特殊的，其分布规律如图所示：

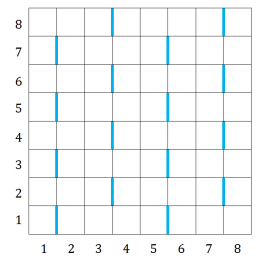
现在有 $n$ 个格子被涂上了颜色，擦掉一个格子的颜色需要花一定的费用（不一定相同）。

不允许出现这样形状（或翻转后出现这样的情况）的涂色区域出现：

求最少要花多少钱来擦颜色才能满足条件。

题解：

最小割。

考虑如下建图方式：

每个格子先拆成入点和出点，之间连容量为擦去它的价值的边。

红色箭头表示两个格子间有连边，方向为箭头所指。

蓝色圆圈的点和源点相连，黑色圆圈的点和汇点相连。

观察可得，任意一个蓝点和黑点相连的路径，恰是不合法的情况。

我们要花最小的代价删掉一些边，使得蓝点和黑点不连通。

最小割问题，跑最大流即可。

由于这张图层数很少，所以 $10^5$ 的数据可以跑过。

Code：

#include<iostream>
#include<algorithm>
#include<map>
#include<cstring>
#include<queue>
#include<cstdio>
using namespace std;
typedef long long LL;
const int N=2e5+5;
const LL inf=0x3f3f3f3f3f3f3f3f;
queue<int>q;
struct edge{
    int to,nxt;LL cap;
}e[N*10];
int head[N],cnt=1,C,R,n,X[N],Y[N],W[N],T,dep[N],iter[N];
bool vis[N];
inline void addedge(int u,int v,LL cap){
    e[++cnt]=(edge){v,head[u],cap},head[u]=cnt;
    e[++cnt]=(edge){u,head[v],0},head[v]=cnt;
}
map<int,int>st[N];
bool bfs(){
    memset(dep,0,sizeof(int)*(T+1));
    dep[0]=1;
    q.push(0);
    while(!q.empty()){
        int u=q.front();q.pop();
        for(int i=head[u];i;i=e[i].nxt)
        if(e[i].cap&&!dep[e[i].to]){
            dep[e[i].to]=dep[u]+1;
            q.push(e[i].to);
        }
    }
    return dep[T];
}
LL dfs(int u,LL f){
    if(u==T||!f)return f;
    for(int&i=iter[u];i;i=e[i].nxt)
    if(e[i].cap&&dep[e[i].to]>dep[u]){
        LL d=dfs(e[i].to,min(f,e[i].cap));
        if(d){
            e[i].cap-=d,e[i^1].cap+=d;
            return d;
        }
    }
    return 0;
}
int main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>C>>R>>n;
    T=2*n+1;
    for(int i=1;i<=n;++i){
        cin>>X[i]>>Y[i]>>W[i];
        addedge(i,i+n,W[i]);
        st[X[i]][Y[i]]=i;
    }
    for(int i=1;i<=n;++i)
    if((X[i]%4==1)&&(Y[i]%2==1)){
        int x=X[i],y=Y[i];
        int id=st[x-1][y];
        if(id){
            if(!vis[id])vis[id]=1,addedge(0,id,inf);
            addedge(id+n,i,inf);
        }
        id=st[x][y-1];
        if(id){
            if(!vis[id])vis[id]=1,addedge(0,id,inf);
            addedge(id+n,i,inf);
        }
        id=st[x][y+1];
        if(id){
            if(!vis[id])vis[id]=1,addedge(0,id,inf);
            addedge(id+n,i,inf);
        }
        id=st[x+1][y];
        if(id){
            addedge(i+n,id,inf);
        }
        ++x;
        int iid=id;
        if(!iid)continue;
        id=st[x][y-1];
        if(id){
            if(!vis[id])vis[id]=1,addedge(id+n,T,inf);
            addedge(iid+n,id,inf);
        }
        id=st[x][y+1];
        if(id){
            if(!vis[id])vis[id]=1,addedge(id+n,T,inf);
            addedge(iid+n,id,inf);
        }
        id=st[x+1][y];
        if(id){
            if(!vis[id])vis[id]=1,addedge(id+n,T,inf);
            addedge(iid+n,id,inf);
        }
    }else
    if((X[i]%4==0)&&(Y[i]%2==0)){
        int x=X[i],y=Y[i];
        int id=st[x+1][y];
        if(id){
            if(!vis[id])vis[id]=1,addedge(0,id,inf);
            addedge(id+n,i,inf);
        }
        id=st[x][y-1];
        if(id){
            if(!vis[id])vis[id]=1,addedge(0,id,inf);
            addedge(id+n,i,inf);
        }
        id=st[x][y+1];
        if(id){
            if(!vis[id])vis[id]=1,addedge(0,id,inf);
            addedge(id+n,i,inf);
        }
        id=st[x-1][y];
        if(id){
            addedge(i+n,id,inf);
        }
        --x;
        int iid=id;
        if(!iid)continue;
        id=st[x][y-1];
        if(id){
            if(!vis[id])vis[id]=1,addedge(id+n,T,inf);
            addedge(iid+n,id,inf);
        }
        id=st[x][y+1];
        if(id){
            if(!vis[id])vis[id]=1,addedge(id+n,T,inf);
            addedge(iid+n,id,inf);
        }
        id=st[x-1][y];
        if(id){
            if(!vis[id])vis[id]=1,addedge(id+n,T,inf);
            addedge(iid+n,id,inf);
        }
    }
    LL flow=0;
    while(bfs()){
        memcpy(iter,head,sizeof(int)*(T+1));
        while(int f=dfs(0,inf))flow+=f;
    }
    cout<<flow<<'\n';
    return 0;
}