【Codeforces 675E】Trains and Statistic

mrsrz 11月 14, 2019

贪心？

题目大意：

有 $1\sim n$ 这 $n$ 个位置，对于 $i\in[1,n-1]$，有 $a_i\in[i+1,n]$，表示 $i$ 可以花费 $1$ 的代价走到 $[i+1,a_i]$ 的任意一个位置。

令 $d_{i,j}$ 表示 $i$ 到 $j$ 的最小花费，求 $\sum\limits_{i=1}^{n-1}\sum\limits_{j=i+1}^{n} d_{i,j}$ 的值。

题解：

按照起点从后往前依次考虑。

对于每个位置出发，我们要使其每一步能走的范围尽可能大。

那么，我们如果能走到 $[l,r]$，为了下一步能走得更远，我们需要在 $[l,r]$ 中选取一个 $a_i$ 最大的 $i$。

这个就是个区间 RMQ 问题。不难在 $O(n\log n)$ 的复杂度内解决。

那么怎么计算贡献呢？

我们考虑对位置 $i$，其第一次走的最大位置为 $k$，从 $k$ 的信息直接转移到 $i$ 的信息。

令 $f_i=\sum\limits_{j=i}^n d_{i,j}$.

考虑 $f_i$ 与 $f_k$ 的关系。如图：

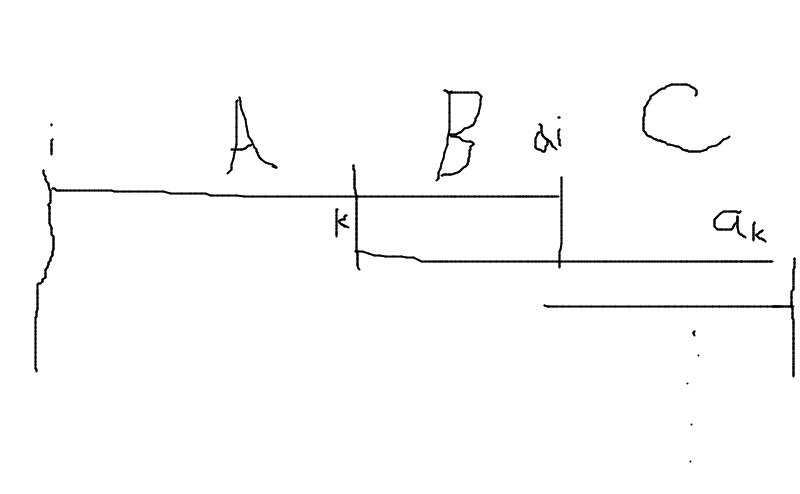
其中，A 段是 $f_i$ 比 $f_k$ 多走的部分，C 段是 $i$ 直接走无法走到，需要走到 $k$ 再往后继续走的。所以 A 段和 C 段的每个数都要多计算 $1$ 的贡献。

$f_i=f_k+(k-i)+(n-a_i)$

上式的意思就是分别加上了 A 段和 C 段的贡献。

最后的答案就是所有 $f_i$ 之和。

时间复杂度就是 RMQ 部分的 $O(n\log n)$。这里的 RMQ 不需要使用 ST 表、线段树等算法，可以使用单调栈维护，查询直接二分即可。

Code：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
const int N=1e5+6;
typedef long long LL;
int n,a[N];
LL ans,f[N];
vector<int>vec;
int main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n;
    for(int i=1;i<n;++i)
        cin>>a[i];
    f[n-1]=ans=1;
    vec.push_back(n-1);
    for(int i=n-2;i;--i){
        int k=*(upper_bound(vec.rbegin(),vec.rend(),a[i])-1);
        f[i]=f[k]+(k-i)+(n-a[i]);
        ans+=f[i];
        while(!vec.empty()&&a[i]>=a[vec.back()])vec.pop_back();
        vec.push_back(i);
    }
    cout<<ans<<endl;
    return 0;
}