【Codeforces 578F】Mirror Box | Mrsrz's blog

矩阵树定理，高斯消元。

题目大意：

给定一个 $n\times m$ 的网格，每个格子上要放 \ 或 / 的镜子。

一个合法的网格需要满足从任意一个边界段垂直射进网格中，光线会从相邻的边界段射出，同时网格中的每一段都被至少一条光线穿透。

以下两种情况属于相邻条件。

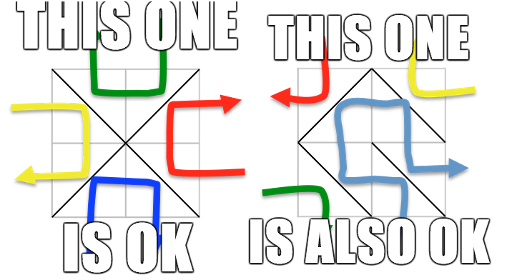
现在有一些镜子没有放，求有多少种不同的放镜子的方法满足条件。

题解：

把镜子看成边，网格的交点为点，并对点奇偶染色，形成二分图。一个格子的镜子连接两个同色的点。

考虑下图的情况（图片来自 yhx-12243）：

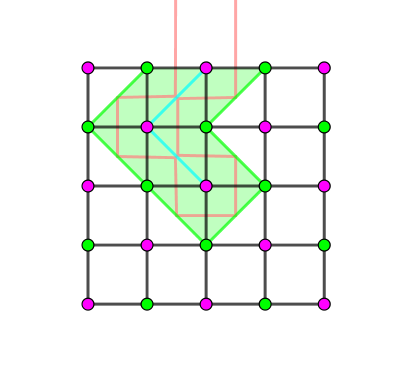
其中绿色边和青色边围成的封闭部分，恰好连接了两个相邻边界。而绿色的边形成树的形态。对于一种绿色边的选法，青色边的选法唯一确定。

由于选择一个绿色点连镜子后，要从边界射出一定得选择另一个绿色点连镜子回来，因此如果绿色点形成一棵树，则一定是一棵完整的生成树。否则无法满足条件。

绿色点本身不能围成环，否则环内的点无法被光线照射。

红色点同理。

因此相当于求两张图的生成树个数。使用矩阵树定理，高斯消元即可。

考虑原来存在边的情况。我们先用并查集把所有连通块求出来，然后再把连通块当结点求生成树个数即可。

时间复杂度 $O(nm\alpha(nm)+k^3)$。

Code：

#include<cstdio>
#include<vector>
#include<algorithm>
#define quit {puts("0");return 0;}
using namespace std;
typedef long long LL;
const int N=405;
int n,m,md;
char mp[N][N];
int fa[N*N];
int b[2][N][N],bel[N*N],tot[2];
bool tp[N*N];
vector<unsigned>ve;
inline int id(int x,int y){return(m+1)*x+y;}
inline int find(int x){while(x!=fa[x])x=fa[x]=fa[fa[x]];return x;}
inline int pow(int a,int b=md-2){
    int ret=1;
    for(;b;b>>=1,a=(LL)a*a%md)if(b&1)ret=(LL)ret*a%md;
    return ret;
}
inline bool merge(int x,int y){
    x=find(x),y=find(y);
    if(x==y)return 0;
    fa[y]=x;
    return 1;
}
void addedge(int(*A)[N],int u,int v){
    --A[u][v],--A[v][u],++A[v][v],++A[u][u];
}
int gauss(int(*A)[N],int n){
    for(int i=1;i<=n;++i)
    for(int j=1;j<=n;++j)
    A[i][j]=(A[i][j]%md+md)%md;
    int ans=1;
    for(int i=1;i<=n;++i){
        int p=0;
        for(int j=i;j<=n&&!p;++j)if(A[j][i])p=j;
        if(!p)return 0;
        if(p!=i)
        for(int j=i;j<=n;++j)swap(A[i][j],A[p][j]);
        if(p!=i)ans=md-ans;
        const int iv=pow(A[i][i]);
        ans=(LL)ans*A[i][i]%md;
        for(int j=i;j<=n;++j)A[i][j]=(LL)A[i][j]*iv%md;
        for(int j=i+1;j<=n;++j){
            const int x=A[j][i];
            A[j][i]=0;
            for(int p=i+1;p<=n;++p)
            A[j][p]=(A[j][p]-(LL)A[i][p]*x%md+md)%md;
        }
    }
    return ans;
}
int main(){
    scanf("%d%d%d",&n,&m,&md);
    const int K=(n+1)*(m+1);
    for(int i=0;i<n;++i)
    scanf("%s",mp[i]);
    for(int i=0;i<K;++i)fa[i]=i;
    for(int i=0;i<=n;++i)
    for(int j=0;j<=m;++j)tp[id(i,j)]=(i^j)&1;
    for(int i=0;i<n;++i)
    for(int j=0;j<m;++j)
    switch(mp[i][j]){
        case'\\':{
            if(!merge(id(i,j),id(i+1,j+1)))quit;
            break;
        }
        case'/':{
            if(!merge(id(i+1,j),id(i,j+1)))quit;
            break;
        }
        case'*':{
            ve.push_back((unsigned)id(i,j)<<16|id(i+1,j+1));
            ve.push_back((unsigned)id(i,j+1)<<16|id(i+1,j));
            break;
        }
    }
    for(int i=0;i<K;++i)
    if(find(i)==i)bel[i]=++tot[tp[i]];
    for(int i=0;i<K;++i)bel[i]=bel[find(i)];
    for(unsigned x:ve){
        int u=x>>16,v=x&65535;
        addedge(b[tp[u]],bel[u],bel[v]);
    }
    int ans=(gauss(b[0],tot[0]-1)+gauss(b[1],tot[1]-1))%md;
    printf("%d\n",ans);
    return 0;
}