【Codeforces 449E】Jzzhu and Squares
数论,推式子
题目大意:
给定 $n\times m$ 的网格图,求所有的四个顶点都是整点的正方形中,包含的完整的 $1\times 1$ 的方格的总个数。
多组数据。
题解:
以下都默认 $n\leq m$
令 $f(n)$ 表示 $n\times n$ 的网格中,所有四个顶点都在网格边缘的正方形包含的完整小方格个数。
那么有 $ans=\sum\limits_{i=1}^n (n-i+1)(m-i+1)f(i)$。
考虑如何求 $f(n)$。
四个顶点都在 $n\times n$ 的网格的角落时,产生 $n^2$ 的贡献。考虑均不在角落的情况。如图所示。
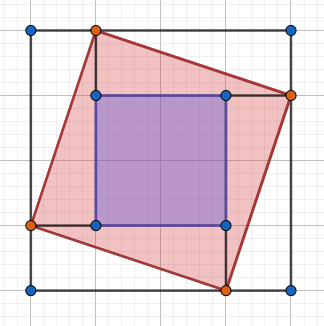
其中,红色的正方形(包括紫色部分)是我们当前在考虑贡献的正方形。我们将其分成紫色的小正方形和四个红色的三角形的贡献分别考虑。
令当前三角形的一条边为 $x$,则另一条边为 $n-x$。
那么中间的正方形的边长就为 $|n-2x|$,贡献为 $(n-2x)^2$。
考虑四个直角三角形的贡献。
以左上角的红色三角形为例,我们发现,一个恰好在三角形内部或者斜边上的点,对应着一个图形内部的完整小正方形,这个小正方形的左上角就是这个点。
所以相当于求一个三角形内部的点和斜边上的点的总个数。
根据皮克定理,设多边形内部的点有 $a$ 个,恰在边上的点有 $b$ 个,那么所有顶点都是整点的多边形的面积为 $a+\frac b 2-1$。
我们令 $g(n,m)$ 表示两条直角边为 $n$ 和 $m$ 的直角三角形的贡献。
那么其边上的点的个数为 $\gcd(n,m)+n+m$,所以内部的点的个数为 $\frac{nm+2-\gcd(n,m)-n-m}2$。而边上的点的个数(不含两端)为 $\gcd(n,m)-1$。
因此 $g(n,m)=\frac{nm-n-m-\gcd(n,m)}{2}$
接下来推 $f(n)$。
其中 $h(n)=\sum\limits_{i=1}^n\gcd(i,n-i)$.
上面的每个求和部分都可以前缀和预处理,考虑如何求 $h(n)$。
所以线性筛,然后狄利克雷卷积即可。时间复杂度 $O(n\log n)$。
现在 $f(n)$ 求出来了。
但是多组数据,所以我们需要 $O(1)$ 求答案。
而 $\sum\limits_{i=1}^n(n-i+1)^2f(i)$ 和 $\sum\limits_{i=1}^n (n-i+1)f(i)$ 都可以线性预处理。
因此可以做到 $O(1)$ 单次查询。
Code:
#include<iostream>
using namespace std;
const int N=1e6+5,md=1e9+7,n=1e6+1;
typedef long long LL;
int F[N],S[N],T[N],P[N];
int phi[N],h[N],pr[N],tot,pri[N/10],pf[N];
bool vis[N];
inline void upd(int&a){a+=a>>31&md;}
inline int calc(int x){return((x+1LL)*x>>1)%md;}
void init(){
phi[1]=1;
for(int i=2;i<=n;++i){
if(!vis[i])pri[++tot]=i,phi[i]=i-1;
for(int j=1;j<=tot&&i*pri[j]<=n;++j){
vis[i*pri[j]]=1;
if(i%pri[j]==0){
phi[i*pri[j]]=phi[i]*pri[j];
break;
}
else
phi[i*pri[j]]=phi[i]*(pri[j]-1);
}
}
for(int i=1;i<=n;++i)
for(int j=i;j<=n;j+=i)
h[j]=(h[j]+(LL)i*phi[j/i])%md;
pf[1]=1,pf[2]=5;
pr[1]=1,pr[2]=4;
for(int i=3;i<=n;++i){
pr[i]=(pr[i-2]+(LL)i*i+(i-2LL)*(i-2))%md;
pf[i]=(pf[i-1]+(LL)i*i)%md;
}
}
int main(){
init();
for(int i=1;i<=n;++i)
F[i]=(pr[i]+2LL*i*calc(i-1)-2LL*pf[i-1]+4LL*md-2LL*i*(i-1)%md+2LL*h[i]-2*i)%md;
for(int i=1,s=0;i<=n;++i)S[i]=((LL)S[i-1]+s+F[i])%md,s=(s+2LL*F[i])%md;
for(int i=1,t=0;i<=n;++i)P[i]=((LL)P[i-1]+t+F[i])%md,upd(t+=F[i]-md);
for(int i=1;i<=n;++i)upd(T[i]=T[i-1]+S[i]-md);
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t;
for(cin>>t;t--;){
int n,m;
cin>>n>>m;
if(n>m)n^=m^=n^=m;
int ans=(T[n]+P[n]*(LL)(m-n))%md;
cout<<ans<<'\n';
}
return 0;
}
