【Codeforces 1172D】Nauuo and Portals
构造题
题目大意:
给定 $n\times n$ 的图,并给定 $2n$ 个限制。
定义左上角为 $(0,0)$。
前 $n$ 个限制 $p_1,p_2,\dots,p_n$ 表示从 $(i,0)$ 出发的人一直往右走,要走到 $(p_i,n+1)$。
后 $n$ 个限制 $q_1,q_2,\dots,q_n$ 表示从 $(0,i)$ 出发的人一直往下走,要走到 $(n+1,q_i)$。
保证 $p,q$ 为 $1\sim n$ 的一个排列。
现在可以放置若干对传送门,每对传送门是两个坐标 $(x_1,y_1),(x_2,y_2)$,表示一个人走到 $(x_1,y_1)$ 后会瞬移到 $(x_2,y_2)$,走到 $(x_2,y_2)$ 后会瞬移到 $(x_1,y_1)$,即双向通行。并且通过传送门不改变行走方向。必须满足 $1\leq x_1,x_2,y_1,y_2\leq n$ 且同一个位置最多一个传送门。
要求输出一组合法的安放传送门的方案,使得所有 $2n$ 个限制均满足。
题解:
考虑把 $n\times n$ 的问题转化为 $(n-1)\times(n-1)$ 的问题。
以最开始为例,我们考虑要走到 $(1,n+1)$ 的人所在行 $p$ 和要走到 $(n+1,1)$ 的人所在列 $q$。
那么我们如图所示,建造传送门 $(p,1),(1,n)$ 以及 $(1,q),(n,1)$。
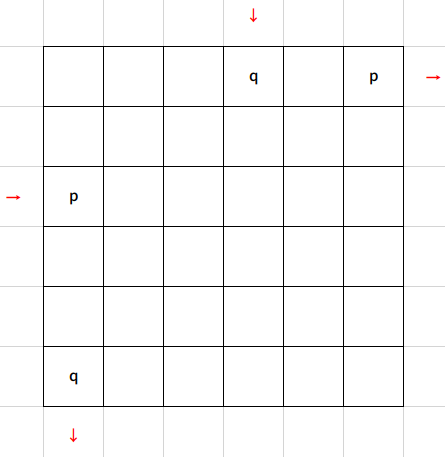
那么,行 $p$ 和列 $q$ 的人显然能够走到它的合法位置,而原来在第一行的人将会到第 $n$ 行,第 $n$ 行的人将会到第 $p$ 行。同理在第一列的人将会到第 $n$ 列,第 $n$ 列的人将会到第 $q$ 列。
再考虑一些特殊情况,如下图。
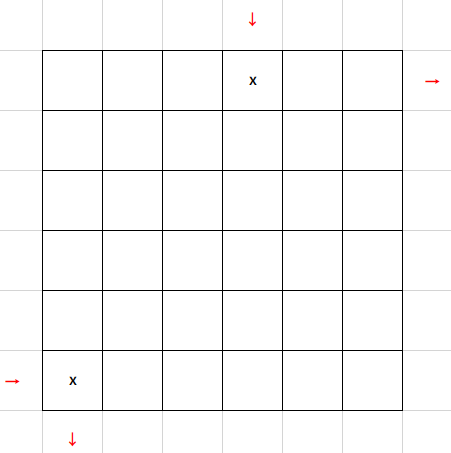
表示有一个人是从第 $n$ 行走到第一行(或者第 $n$ 列走到第一列,同理)。那么只需要开一对传送门即可。
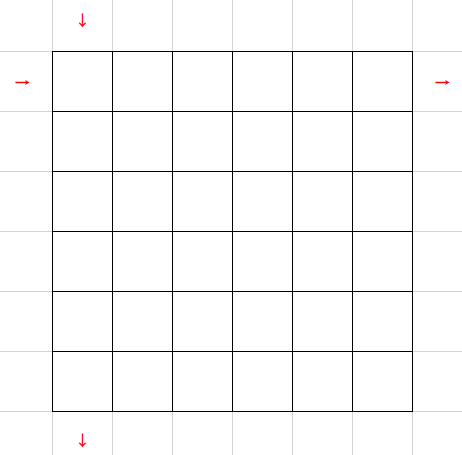
这种情况就无需开传送门了。
以上,我们花费了 $0\sim 2$ 扇传送门,使得最终到第一行和第一列的人满足了条件,并令第 $2\sim n$ 行和 $2\sim n$ 列都保持每行/列有且仅有一个人。那么我们就转化为了一个 $(n-1)\times (n-1)$ 的子问题。继续按照上述方法讨论即可。到 $1\times 1$ 的时候停止。
时间复杂度 $O(n)$。
Code:
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1005;
int n,R[N],C[N],top,iR[N],iC[N];
struct doors{
int r1,c1,r2,c2;
}d[N<<1];
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;++i)cin>>R[i],iR[R[i]]=i;
for(int i=1;i<=n;++i)cin>>C[i],iC[C[i]]=i;
for(int i=1;i<n;++i){
if(R[i]==i&&C[i]==i)continue;
if(iR[i]==n&&iC[i]==n){
d[++top]=(doors){i,n,n,i};
R[n]=R[i],C[n]=C[i];
iR[R[n]]=n;iC[C[n]]=n;
continue;
}
if(iC[i]==n){
d[++top]=(doors){iR[i],i,i,n};
C[n]=C[i];iC[C[n]]=n;
R[iR[i]]=R[i],iR[R[iR[i]]]=iR[i];
continue;
}
if(iR[i]==n){
d[++top]=(doors){i,iC[i],n,i};
R[n]=R[i];iR[R[n]]=n;
C[iC[i]]=C[i],iC[C[iC[i]]]=iC[i];
continue;
}
d[++top]=(doors){iR[i],i,i,n},
d[++top]=(doors){i,iC[i],n,i};
int r=iR[i],c=iC[i];
R[r]=R[n],R[n]=R[i];
C[c]=C[n],C[n]=C[i];
iR[R[r]]=r,iC[C[c]]=c;
iR[R[n]]=n,iC[C[n]]=n;
}
cout<<top<<'\n';
for(int i=1;i<=top;++i)
cout<<d[i].r1<<' '<<d[i].c1<<' '<<d[i].r2<<' '<<d[i].c2<<'\n';
return 0;
}
