【AtCoder Grand Contest 021 E】Ball Eat Chameleons
组合数学,贪心。
题目大意:
有 $n$ 条变色龙和 $k$ 个球。变色龙和球都有红色和蓝色。变色龙初始都为蓝色。
一条变色龙最后是红色,必须满足下列条件之一。
- 它吃过的红球的个数大于蓝球个数。
- 它吃过的红球个数等于蓝球个数,且最后一个吃的是蓝球。
你可以按顺序指定每个球为红色还是蓝色,然后任意喂给变色龙。
求有多少不同的球的颜色序列,满足这种颜色序列存在一种喂食方式,可以让所有变色龙最后都变成红色(注意只要求颜色序列,和喂哪只变色龙没有关系)。
题解:
令红球有 $R$ 个,蓝球有 $B$ 个。
首先,$R\lt B$ 不可能,因为至少存在一只变色龙,它吃的蓝球个数比红球多。
考虑对于给定的 $R,B$,它相当于从 $(0,0)$ 走到 $(R,B)$,每步只能向上(吃红球)或向右(吃蓝球)走的方案数。即 $\binom{R+B}{R}$。
考虑以下两种情况:
$R=B$,此时所有变色龙吃的红球和蓝球个数相同,所以最后一个吃的一定是蓝球。转化为 $(R,B-1)$ 的问题,即另一种情况。
$R\gt B$。若 $R-B\geq n$,则我们可以使任意一只变色龙吃的红色球都比蓝色球多。所以方案数就是 $\binom{R+B}{B}$。
若 $R-B\lt n$,则有 $n-(R-B)$ 只变色龙吃的红色球和蓝色球个数相等。那么对于颜色序列的每个前缀,蓝球比红球多的个数不能超过 $B-[n-(R-B)]=R-n$。
那么,相当于从 $(0,0)$ 走到 $(R,B)$,不能穿过直线 $y=x+R-n$,相当于不能碰到直线 $y=x+R-n+1$。
考虑这种东西的方案数怎么求。
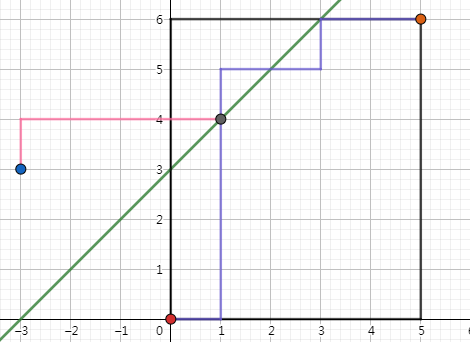
如图,我们要求红点走到橙点的方案数。紫色路径是其中一条走法。
考虑其第一次碰到绿色直线的点(灰点)。
我们将红点以及红点到灰点的子路径沿绿色直线翻折,得到蓝点和粉色路径。
容易发现,原来红点到橙点,碰到绿色直线的所有方案,和蓝点到橙点的方案一一对应。这样就可以计算不合法方案了。
于是这部分的方案数就是 $\binom{R+B}{B}-\binom{R+B}{2R-n+1}$。
枚举 $R$ 然后直接计算即可。
时间复杂度 $O(n+k)$。
Code:
#include<cstdio>
#include<algorithm>
typedef long long LL;
const int N=1e6+2,md=998244353;
int n,k,fac[N],iv[N],ans;
inline void upd(int&a){a+=a>>31&md;}
inline int C(int n,int m){return(n>=m)?(LL)fac[n]*iv[m]%md*iv[n-m]%md:0;}
inline int calc(int R,int B){
int r=C(R+B,R);
if(R-B<n)upd(r-=C(R+B,2*R-n+1));
return r;
}
int main(){
scanf("%d%d",&n,&k);
for(int i=*fac=1;i<N;++i)fac[i]=(LL)fac[i-1]*i%md;
iv[N-1]=741754199;
for(int i=N-2;~i;--i)iv[i]=(i+1LL)*iv[i+1]%md;
for(int R=std::max(k+1>>1,n);R<=k;++R)upd(ans+=calc(R,R==k-R?R-1:k-R)-md);
printf("%d\n",ans);
return 0;
}
