【AtCoder Grand Contest 008 E】Next or Nextnext
动态规划,数数。
题目大意:
给定一个长度为 $n$ 的序列 $a_1,a_2,a_3,\ldots,a_n$。
询问有多少个长度为 $n$ 的排列 $p$ 满足对于所有 $i$,都有 $p_i=a_i$ 或者 $p_{p_i}=a_i$。
题解:
对一个排列,我们连边 $i\rightarrow p_i$ 可以得到一张由若干个环组成的图。
我们现在连边 $i\rightarrow a_i$,观察一下这张图和排列的图直接的关系。
其区别在于,有的边是 $i\rightarrow p_{p_i}$ 的。
下面引用官方题解的图来讨论。
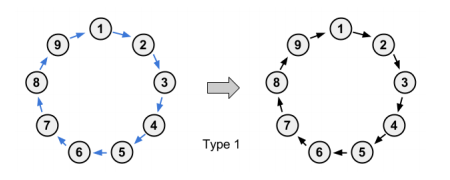
第一种情况,这个连通块所有边都是形如 $i\rightarrow p_i$ 的,那么环保持不变。
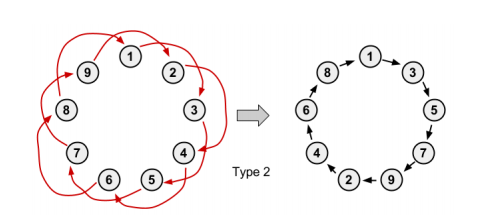
第二种情况,这个连通块所有边都是形如 $i\rightarrow p_{p_i}$ 的,且原来环上的点的个数是奇数。则它会形成一个新的环。

第三种情况,这个连通块所有边都是形如 $i\rightarrow p_{p_i}$ 的,且原来环上的点的个数是偶数。则它会形成两个新的环,点数为原来的一半。

第三种情况,这个连通块两种边都有。那么,它会形成一棵基环内向树,并且是环加上若干条链的形式(一个环上的点最多连入一条链)。
我们得到的是变换后的图,这个图会由若干环和若干基环树组成。
我们分别对环和基环树进行考虑。
对于环,它有以下变化方式:
- 什么都不动(第一种情况)。
- 一个奇环,变化为第二种情况之前的状态。这个奇环大小不能为 $1$,否则和方式 1 算重。
- 两个大小相等的环,变化为第三种情况之前的状态。这里大小为 $k$ 的两个环,有 $k$ 种不同的还原方案(固定一个环不动,另一个环旋转)。
环的部分可以通过 dp 进行计数。
接下来考虑基环树的部分。我们对于一条长度为 $l_1$ 的链,其连接到奇环上的点,和下一个有链连接的奇环上的点之间的边数为 $l_2$。
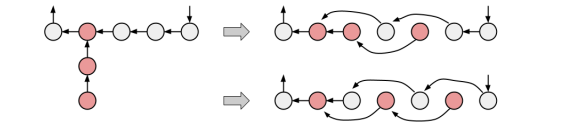
如图所示,我们要把红色结点嵌入这些边中间。
我们只需要讨论链和环连接的那个点的后面的位置放环点还是链点就好了。只要确定了这个点,那么接下来一定是环点、链点循环(最后可能有多余的一连串环点,但不能是多余的一连串链点,否则会和后面一条链冲突)。
那么,若 $l_1\gt l_2$,则无合法方案。若 $l_1=l_2$,则只有一种合法方案。若 $l_1\lt l_2$,则有两种合法方案。用乘法原理计算即可。
时间复杂度 $O(n)$。
Code:
#include<cstdio>
#include<cstdlib>
#include<cassert>
typedef long long LL;
const int md=1e9+7,N=1e5+5;
int tot[N],n,a[N],deg[N],cnt,bel[N],L[N],ans=1,top[N];
bool vis[N],inc[N];
inline void fail(){puts("0");exit(0);}
inline void upd(int&a){a+=a>>31&md;}
int solve(int L){
static int f[N];
*f=1;
for(int i=1;i<=tot[L];++i){
if((L&1)&&(L>1))upd(f[i]=f[i-1]*2-md);else f[i]=f[i-1];
if(i>1)f[i]=(f[i]+(i-1LL)*f[i-2]%md*L)%md;
}
return f[tot[L]];
}
int solve_tree(int id){
int len=0,now=top[id],r=1;
do{
++len;
now=a[now];
if(L[now]){
if(L[now]>len)return 0;
if(L[now]<len)upd(r=r*2-md);
len=0;
}
}while(now!=top[id]);
return r;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i)scanf("%d",a+i),++deg[a[i]];
for(int i=1;i<=n;++i)
if(deg[i]==2&&!vis[i]){
int j;
top[bel[i]=++cnt]=i;
vis[i]=inc[i]=1;
for(j=a[i];!vis[j];j=a[j])vis[j]=1,bel[j]=cnt,inc[j]=1;
if(j!=i)fail();
}else if(deg[i]>2)fail();
for(int i=1;i<=n;++i)
if(!vis[i]&°[i]==0){
int x=i;
while(!vis[x])x=a[x];
if(!inc[x]||L[x])fail();
int len=0;
for(x=i;!inc[x];x=a[x])vis[x]=1,++len;
L[x]=len;
}
for(int i=1;i<=n;++i)if(!vis[i]){
assert(deg[i]==1),vis[i]=1;
int x,len=1;
for(x=a[i];!vis[x];x=a[x])vis[x]=1,++len;
assert(x==i);
++tot[len];
}
for(int i=1;i<=n;++i)if(tot[i])ans=(LL)ans*solve(i)%md;
for(int i=1;i<=cnt;++i)
ans=(LL)ans*solve_tree(i)%md;
printf("%d\n",ans);
return 0;
}
